Question

【题目】已知△ABC中，AC＝BC，∠C＝100°，AD平分∠BAC交BC于D，点E为AB上一点，且∠EDB＝∠B．求证：AB＝AD+CD．

Answer 1

【答案】见解析

【解析】

由∠C＝100°，AC＝BC得到∠B＝∠CAB＝40°，再由∠EDB＝∠B得到∠DEB＝100°，BE＝DE，则∠AED＝80°，然后根据角平分线的定义得∠DAE＝20°，于是利用三角形内角和定理可计算出∠ADE＝80°，所以AD＝AE，于是AB＝AE＋BE＝AD＋CD．

∵∠C＝100°，AC＝BC，
∴∠B＝∠CAB＝40°，
∵∠EDB＝∠B，
∴∠DEB＝100°，BE＝DE，
∴∠AED＝80°，
∵AD平分∠BAC，
∴∠DAE＝∠DAF＝20°，
∴∠ADE＝180°80°20°＝80°，
∴AD＝AE，
过点D作DF⊥AC于点F，作DH⊥AB于点H，

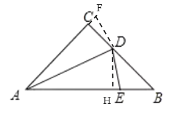
∴DF＝DH，
在△CDF和△EDH中，
∵

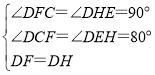
∴△CDF≌△EDH（AAS），
∴CD＝DE，
∴CD＝BE，
∴AB＝AE＋BE＝AD＋CD．