Question

4．如图，在边长为$\sqrt{3}$+1的菱形ABCD中，∠A=60°，点E，F分别在AB，AD上，沿EF折叠菱形，使点A落在BC边上的点G处，且EG⊥BD于点M，则EG的长为$\sqrt{3}$．

Answer 1

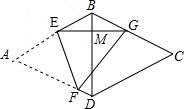
分析 首先连接AC，在Rt△ABO中，求出AO的长度，进而求出AC的长度是多少；然后根据EG⊥BD，AC⊥BD，可得EG∥AC，所以$\frac{EG}{AC}=\frac{BE}{AB}$，据此求出EG的长为多少即可．

解答 解：如图1，连接AC，交BD于点O，，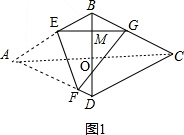
∵四边形ABCD是菱形，
∴AC⊥BD，AC=2AO，
∵∠A=60°，
∴∠BAO=30°，
∴AO=AB•cos30°=（$\sqrt{3}$+1）×$\frac{\sqrt{3}}{2}$=$\frac{3+\sqrt{3}}{2}$，
∴AC=$\frac{3+\sqrt{3}}{2}$×2=3$+\sqrt{3}$，
∵沿EF折叠菱形，使点A落在BC边上的点G处，
∴EG=AE，
∵EG⊥BD，AC⊥BD，
∴EG∥AC，
∴$\frac{EG}{AC}=\frac{BE}{AB}$，
又∵EG=AE，
∴$\frac{EG}{3+\sqrt{3}}=\frac{\sqrt{3}+1-EG}{\sqrt{3}+1}$，
解得EG=$\sqrt{3}$，
∴EG的长为$\sqrt{3}$．
故答案为：$\sqrt{3}$．

点评 （1）此题主要考查了翻折变换问题，要熟练掌握，解答此题的关键是要明确：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
（2）此题还考查了菱形的性质和应用，要熟练掌握，解答此题的关键是要明确：①菱形具有平行四边形的一切性质；②菱形的四条边都相等；③菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；④菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．