
分析 同意小明的说法,原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,判断即可.
解答 解:同意小明的说法,理由为:
原式=[$\frac{a+2}{a(a-2)}$-$\frac{a-1}{(a-2)^{2}}$]•$\frac{a}{a-4}$=$\frac{(a+2)(a-2)-a(a-1)}{a(a-2)^{2}}$•$\frac{a}{a-4}$=$\frac{a-4}{a(a-2)^{2}}$•$\frac{a}{a-4}$=$\frac{1}{(a-2)^{2}}$,
∵(a-2)2≥0,且a-2≠0,
∴(a-2)2>0,即$\frac{1}{(a-2)^{2}}$一定为正数,
则在原分式有意义的前提下,分式的值一定是正数.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
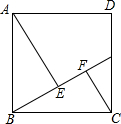 如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.
如图,正方形ABCD的边长是10,点G是CD边上任意一点,AE⊥BG于点E,CF⊥BG于点F,AE=8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②当AD=2时,EF与半圆相切;③线段EF的最小值为4;④若点F恰好落在BC上,则AD=4.其中正确结论的序号是①②.
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②当AD=2时,EF与半圆相切;③线段EF的最小值为4;④若点F恰好落在BC上,则AD=4.其中正确结论的序号是①②.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
| 0<x≤200 | a |
| 200<x≤400 | b |
| x>400 | 0.92 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com