
 一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )
一架2.5米长的梯子底部距离墙脚0.7米,若梯子的顶端下滑0.4米,那么梯子的底部在水平方向滑动了( )| A. | 1.5米 | B. | 0.9米 | C. | 0.8米 | D. | 0.5米 |
分析 先根据梯子的顶端下滑了0.4米求出A′C的长,再根据勾股定理求出B′C的长,进而可得出结论.
解答 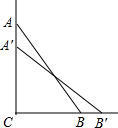 解:(1)∵在Rt△ABC中,AB=2.5m,BC=0.7m,
解:(1)∵在Rt△ABC中,AB=2.5m,BC=0.7m,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{2.{5}^{2}-0.{7}^{2}}$=2.4(m).
∵梯子的顶端下滑了0.4米,
∴A′C=2m,
∵在Rt△A′B′C中,A′B′=2.5m,A′C=2m,
∴B′C=$\sqrt{2.{5}^{2}-{2}^{2}}$=1.5m,
∴BB′=B′C-BC=1.5-0.7=0.8m.
故选C.
点评 此题主要考查了勾股定理的应用,关键是掌握勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
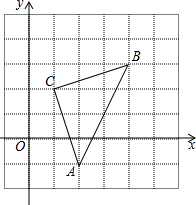 如图,在直角坐标系中△ABC的顶点都在网格点上,其中,C点坐标为(1,2),
如图,在直角坐标系中△ABC的顶点都在网格点上,其中,C点坐标为(1,2),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
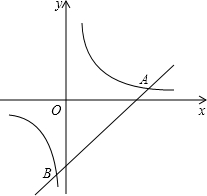 如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.
如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
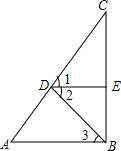 如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
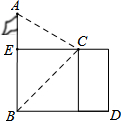 如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么,旗杆AB的高度是( )
如图,某人站在楼顶观测对面的笔直的旗杆AB.已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么,旗杆AB的高度是( )| A. | ($\sqrt{2}$+8$\sqrt{3}$)m | B. | (8+8$\sqrt{3}$)m | C. | (8$\sqrt{2}$+$\frac{8\sqrt{3}}{3}$)m | D. | (8+$\frac{8\sqrt{3}}{3}$)m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com