Question

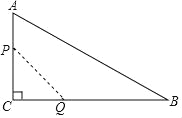
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝12cm，BC＝24cm．动点P从点A开始沿边AC向点C以2cm/s的速度移动；动点Q从点C开始沿边CB向点B以4cm/s的速度移动．如果P，Q两点同时出发．

(1)经过几秒，△PCQ的面积为32cm2？

(2)若设△PCQ的面积为S，运动时间为t，请写出当t为何值时，S最大，并求出最大值；

(3)当t为何值时，以P，C，Q为顶点的三角形与△ABC相似？

Answer 1

【答案】(1) 2秒或4秒；(2) t＝3时，S的最大值为36cm2；(3) t＝3或1.2.

【解析】

（1）根据三角形的面积公式列出方程，解方程得到答案；
（2）根据三角形的面积公式列出函数关系式，根据二次函数的性质解答；
（3）分△PCQ∽△ACB和△PCQ∽△BCA两种情况，根据相似三角形的性质计算即可．

解：(1)设经过x秒，△PCQ的面积为32cm2．

由题意得，PC＝12﹣2t，CQ＝4t，

则(12﹣2t)×4t＝32

解得：x1＝2，x2＝4，

答：经过2秒或4秒，△PCQ的面积为32cm2；

(2)∵出发时间为t，点P的速度为2cm/s，点Q的速度为4cm/s，

∴PC＝12﹣2t，CQ＝4t

∴S＝PCCQ＝(12﹣2t)×4t＝﹣4t2+24t，

S＝﹣4t2+24t＝﹣4(t﹣3)2+36

则t＝3时，S的最大值为36cm2；

(3)当△PCQ∽△ACB时，

＝，即，=

解得，t＝3，

当△PCQ∽△BCA时，

＝，即，=

解得，t＝1.2，

综上所述，当t＝3或1.2时，以P，C，Q为顶点的三角形与△ABC相似．