
【题目】为了加强学生安全教育,某市某中学举行了一次“安全知识竞赛”,共有1600名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面的频数分布表和频数分布直方图,解答下列问题:
频数分布表
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 8 | 0.16 |
70.5~80.5 | 12 | 0.24 |
80.5~90.5 | 15 | 0.30 |
90.5~100.5 | a | b |
合计 |
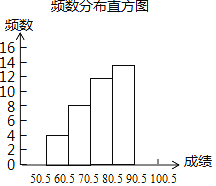
(1)频数分布表中a= ,b= ;
(2)抽取的样本容量是 ,请补全频数分布直方图.
(3)若成绩在80分以上(不含80分)为优秀,则该校成绩没达到优秀的约为多少人?
【答案】(1)11,0.22;(2)50,见解析;(3)该校成绩没达到优秀的约为768人.
【解析】
(1)根据第一组的频数与频率列式求出被抽取的学生总人数,然后减去其它各组的人数即可得到a的值,用a的值除以总人数即可得到b;
(2)根据(1)的计算可得抽取的样本容量是50,并且补全直方图即可;
(3)用学生总人数乘以前三组的频率之和,计算即可得解.
解:(1)被抽取的学生人数为:4÷0.08=50(人),
所以,a=50﹣4﹣8﹣12﹣15=50﹣39=11,
b=![]() =0.22;
=0.22;
故答案为:11;0.22.
(2)由(1)可知,抽取的样本容量是50.
补全频数分布直方图如图所示:
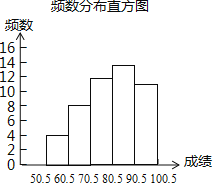
故答案为50;
(3)(0.08+0.16+0.24)×1600=768(人).
答:该校成绩没达到优秀的约为768人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
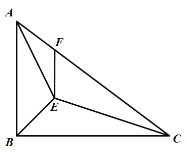
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点E是△ABC的内心,过点E作EF∥AB交AC于点F,则EF的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
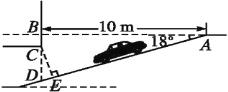
【题目】.某商场为缓解“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5 m.根据规定,地下停车库坡道入口上方要张贴限高标志,以便告知驾驶员所驾车辆能否安全驶入.小明认为CD的长就是所限制的高度,而小亮认为应该以CE的长作为限制的高度.小明和小亮谁说得对?请你判断并计算出正确的结果.(结果精确到0.1 m,参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有_____.(填序号)
①![]() 的平方根是±3
的平方根是±3
②绝对值等于它本身的数一定是正数
③关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是m≤3
④如果一个多边形的内角和是外角和的3倍,则这个多边形的边数是8
⑤观察下列单项式2x,﹣4x2,8x3,﹣16x4,…,则第7个单项式是128x7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣1)2+k的图象与x轴交于A,B两点,AB=4,与y轴交于C点,E为抛物线的顶点,∠ECO=135°.
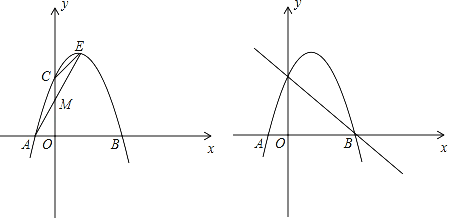
(1)求二次函数的解析式;
(2)若P在第四象限的抛物线上,连接AE交y轴于点M,连接PE交x轴于点N,连接MN,且S△EAP=3S△EMN,求点P的坐标;
(3)过直线BC上两点P,Q(P在Q的左边)作y轴的平行线,分别交抛物线于N,M,若四边形PQMN为菱形,求直线MN的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD表示该产品每千克生产成本y1(单位:元)与产量x(单位:kg)之间的函数关系;线段CD表示每千克的销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义.
(2)求线段AB所表示的y1与x之间的函数表达式.
(3)当0≤x≤90时,销售该产品获得的利润与产量的关系式是 ;当90≤x≤130时,销售该产品获得的利润与产量的关系式是 ;总之,当产量为 kg时,获得的利润最大,最大利润是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在边AB上,以AD为直径的⊙O,与边BC有公共点E,则AD的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com