
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���䶥��ΪP������PA��AC��CP������C��y��Ĵ���l����֪����P������Ϊ��-3��-4�����߶�PC֮��Ϊ3
��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���䶥��ΪP������PA��AC��CP������C��y��Ĵ���l����֪����P������Ϊ��-3��-4�����߶�PC֮��Ϊ3![]()
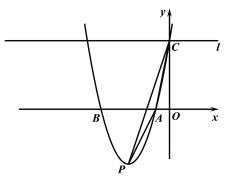
(1)����κ�������ʽ��
(2)MΪֱ��l��һ�㣬����M,C,OΪ���������������A,C,OΪ��������������ƣ���ֱ��д����M�����ꡣ
(3)ֱ��l���Ƿ���ڵ�D��ʹ��PBD�����������PAC�������3���������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1�� ![]() ����2��
����2��![]() ��(3) ���ڣ�
��(3) ���ڣ�![]()
��������
��1�����ù��ɶ������C�����꣬Ȼ�������߽���ʽд�ɶ���ʽ���ٻ�Ϊһ��ʽ����2�����A,B��������꣬���������֪��ACO�͡�MCO��Ϊֱ��������
��Ȼ�����������������������������г�����ʽ���Ӷ���⣨3������ϵ������ֱ��PC�Ľ���ʽΪy=3x+5����ֱ�߽�x����E����E��![]() ��0������ֱ��PQ��x����F����BD=3AFʱ����PBD�����������PAC�������3�������������ηֱ���⼴�ɽ�����⣮
��0������ֱ��PQ��x����F����BD=3AFʱ����PBD�����������PAC�������3�������������ηֱ���⼴�ɽ�����⣮
�⣺��1������P��PH��y��
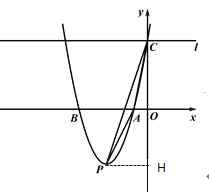
������P��������-3��-4��
��PH=3��OH=4
��OC=x
��Rt��PCH��![]()
��![]()
��ã�![]() ����ֵ��ȥ��
����ֵ��ȥ��
����C��������0,5��
�躯������ʽ![]()
����0,5�����룬![]()
��ã�a=1
�ຯ������ʽΪ![]()
��2����![]() �У���y=0ʱ
�У���y=0ʱ
![]()
��ã�![]()
����A��-1,0����B(-5,0)
��M��ֱ��l��
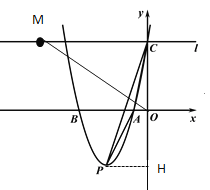
�������֪��ACO�͡�MCO��Ϊֱ��������
��M��x,5��
�൱![]() ʱ����������������
ʱ����������������
��![]()
��ã�![]()
��![]() ʱ����������������
ʱ����������������
��![]()
��ã�![]()
���M������Ϊ![]() ��
��![]() ��
��![]() ��
��![]()
��3����ֱ��PC�Ľ���ʽΪy=kx+b��
����![]()
���![]()
��ֱ��PC�Ľ���ʽy=3x+5��
��ֱ�߽�x����E����E��![]() ��0����
��0����
��ֱ��PD��x����F����BF=3AEʱ����PBD�����������PAC�������3����
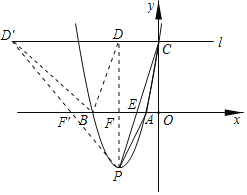
��A(-1,0)��B(-5,0)
��AE=![]() ��
��
��BF=2
��F��-3��0����F'��-7��0��
��F��-3��0��ʱ��ֱ��PF��ֱ��x�ᣬ
��D��-3��5��
��F'��-7��0��ʱ��ֱ��PF'�Ľ���ʽΪy=-x-7��
��D'��-12��5����
�������������������ĵ�D��-3��5����D'��-12��5����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ABCD��һ����OΪֱ�Ƕ��������ǰ壬�ƶ����ǰ壬ʹ���ǰ����ֱ�DZ�����ֱ�߷ֱ���ֱ��BC��CD������M��N��
��1����ͼ1������O���A�غϣ���OM��ON��������ϵ��__________________��
��2����ͼ2������O�������ε����ģ������Խ��ߵĽ���������1���еĽ����Ƿ���Ȼ��������˵��������
��3����ͼ3������O�������ε��ڲ������߽�������OM=ONʱ����̽����O���ƶ������п��γ�ʲôͼ�Σ�
��4����ͼ4�ǵ�O���������ⲿ��һ���������OM=ONʱ������͡���O��λ���ڸ�������£����ⲿ���ƶ����γɵ�ͼ�Ρ����һ����ȷ�Ľ��ۣ�������˵����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������
�ٷ���x2��2x+1��0�ĸ���![]() ������
������![]() ��
��
�ڷ���2x2��x��2��0�ĸ���![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��
�۷���3x2+4x��7��0�ĸ���![]() ��
��![]() ������
������![]() ��
��![]() ��
��
��1���������Ϣ٢ڢ�������룺�������x��һԪ���η���ax2+bx+c��0��a��0��������ʵ����Ϊ![]() ����ô
����ô![]() ��ϵ��a��b��c��ʲô��ϵ����д����IJ��벢֤����IJ��룻
��ϵ��a��b��c��ʲô��ϵ����д����IJ��벢֤����IJ��룻
��2��������IJ�����ۣ������������⣺
��֪����x�ķ���x2+��2k+1��x+k2��2��0��ʵ����![]() ����
����![]() ����k��ֵ
����k��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
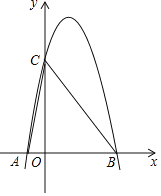
����Ŀ����֪����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ���Ҿ�����
���Ҿ�����![]()
(1)��������ߵĽ���ʽ����������ͶԳ��
(2)�����������Ƿ����һ��![]() ��ʹ
��ʹ![]() �������
�������![]() ��������(��
��������(��![]() �����
�����![]() �غ�)�������ڣ������
�غ�)�������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����κ���ͼ��Ķ�������Ϊ��-1,2������y�ύ���������Ϊ![]()
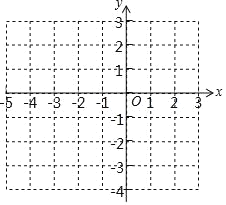
��1����������κ����ı���ʽ��
��2���ڸ�����ֱ������ϵ�У��������������ͼ��
��3�� ��֪����A��-2020��a����B��2019��b���ڴ˶��κ���ͼ���ϣ���Ƚ�a��b�Ĵ�С��a b���ã���������գ�
��4������ͼ��-2��x��2ʱ����ֱ��д��y��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
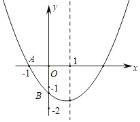
����Ŀ����ͼ����֪���κ���y��ax2+bx+c��a��0����ͼ����x�ύ�ڵ�A����1��0������y��Ľ���B�ڣ�0����2����C��0����1��֮�䣨�����������㣩���Գ���Ϊֱ��x��1�����н��ۣ���abc��0����4a+2b+c��0����4ac��b2��8a����![]() ����b��c�����к�������ȷ���۵�ѡ����_____��
����b��c�����к�������ȷ���۵�ѡ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
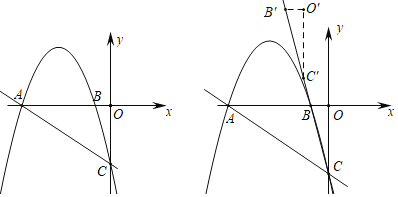
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y����![]() x2��
x2��![]() x��3��x����A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C
x��3��x����A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C
��1����ֱ��AC�Ľ���ʽ��
��2����P��ֱ��AC�Ϸ��������ϵ�һ���㣨�����A����C�غϣ�������P��PD��x�ύAC�ڵ�D����PD�����ֵ��
��3������BOC��ֱ��BCƽ�ƣ���Bƽ�ƺ�Ķ�Ӧ��Ϊ��B�䣬��Oƽ�ƺ�Ķ�Ӧ��Ϊ��O�䣬��Cƽ�ƺ�Ķ�Ӧ��Ϊ��C�䣬��S������ƽ����һ�㣬����A��C��O�䣬SΪ������ı��������Σ�������з��������ĵ�S�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�ADƽ����BAC,�����²�����ͼ����һ�����ֱ��Ե�A��DΪԲ�ģ��Դ���![]() �ij�Ϊ�뾶��AD��������������������M��N;�ڶ���������MN���ֱ�AB��AC�ڵ�E��F��������������DE��DF������BD=6��AF=4��CD=3����BE�ij��ǣ� ��
�ij�Ϊ�뾶��AD��������������������M��N;�ڶ���������MN���ֱ�AB��AC�ڵ�E��F��������������DE��DF������BD=6��AF=4��CD=3����BE�ij��ǣ� ��

A. 2 B. 4 C. 6 D. 8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P��������y��x2��4x+3�ϵ�һ�㣬�Ե�PΪԲ�ġ�1����λ����Ϊ�뾶����P������P��ֱ��y��0����ʱ����P������Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com