

���� ��1������ͳ��ͼ��D����������ӦΪ20��10%��
��2��������λ���������Ķ����Լ�����ͳ��ͼ������ͳ��ͼ���������ݣ���������𰸣�
��3����С��ķ����Ǵӵڶ�����ʼ���ִ���ģ�
�ڸ���ƽ�����ļ��㹫ʽ�������ȷ��ƽ�������ٳ���260���ɵõ������
��� �⣺��1��D��������Ϊ��20��10%=2��3��
��2������Ϊ5����λ��Ϊ5��
��3���ٵڶ�����
��$\overline{x}$=$\frac{4��4+5��8+6��6+7��2}{20}$=5.3�����
������260��ѧ����ֲ��5.3��260=1378���ã���
���� ���⿼��������ͳ��ͼ������ͳ��ͼ���õ���֪ʶ����ƽ��������λ���������Լ��������������壬Ū�������ǽⱾ��Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x+y��2=49 | B�� | x2+y2=65 | C�� | ��x-y��2=81 | D�� | ��xy��2=-64 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
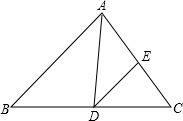 ��ͼ���ڡ�ABC�У���B=46�㣬��ADE=40�㣬ADƽ�֡�BAC����BC��D��DE��AB����AC��E�����C�Ĵ�С�ǣ�������
��ͼ���ڡ�ABC�У���B=46�㣬��ADE=40�㣬ADƽ�֡�BAC����BC��D��DE��AB����AC��E�����C�Ĵ�С�ǣ�������| A�� | 46�� | B�� | 66�� | C�� | 54�� | D�� | 80�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
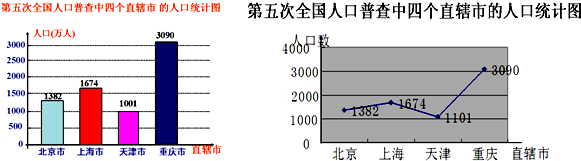
| A�� | ������˿�����������ֱϽ���˿ڵĺ��൱ | |
| B�� | ������˿�������� | |
| C�� | �Ϻ���Ա������˿������İٷ����뱱����������˿������İٷ�����С | |
| D�� | ����������˿�������3����Ҫ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | -2 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$+$\sqrt{3}$ | B�� | $\sqrt{2}$-$\sqrt{3}$ | C�� | -$\sqrt{2}$-$\sqrt{3}$ | D�� | $\sqrt{3}$-$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
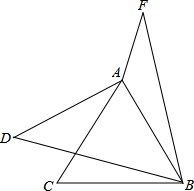 ��ͼ����֪�ȱߡ�ABC����D��AC����࣬��BD�Ƶ�B˳ʱ����ת60����BF����F���D���Ӧ������AF��AD��AD=2����CBD=15�㣬��AFB=30�㣬��AF�ij�Ϊ$\sqrt{6}-\sqrt{2}$��
��ͼ����֪�ȱߡ�ABC����D��AC����࣬��BD�Ƶ�B˳ʱ����ת60����BF����F���D���Ӧ������AF��AD��AD=2����CBD=15�㣬��AFB=30�㣬��AF�ij�Ϊ$\sqrt{6}-\sqrt{2}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com