
【题目】在平面直角坐标系中,A(4,0),直线l:y=6与y轴交于点B,点P是直线l上点B右侧的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P的横坐标满足0≤x≤8,则点Q的运动路径长为_____.
【答案】![]()
【解析】解:如图,过点P作PE⊥OA,垂足为E,过点Q作QF⊥BP,垂足为F.
∵BP∥OA,PE⊥OA,∴∠EPF=∠PEO=90°.
∵∠APQ=90°,∴∠EPA=∠FPQ=90°﹣∠APF.
在△PEA和△PFQ中,∵ ,∴△PEA≌△PFQ(AAS),∴PE=PF,EA=QF,若点P的坐标为(a,6),则PF=PE=6,QF=AE=|4﹣a|,∴点Q的坐标为(a+6,10﹣a).
,∴△PEA≌△PFQ(AAS),∴PE=PF,EA=QF,若点P的坐标为(a,6),则PF=PE=6,QF=AE=|4﹣a|,∴点Q的坐标为(a+6,10﹣a).
∵无论a为何值,点Q的坐标(a+6,10﹣a)都满足一次函数解析式y=﹣x+16,∴点Q始终在直线y=﹣x+16上运动.
当点P的横坐标满足0≤x≤8时,点Q的横坐标满足6≤x≤14,纵坐标满足2≤y≤10,则Q的运动路径长为![]() =8
=8![]() .故答案为:8
.故答案为:8![]() .
.



科目:初中数学 来源: 题型:
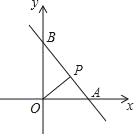
【题目】如图,直线y=3﹣2x与x轴,y轴分别相交于点A,B,点P(x,y)是线段AB上的任意一点,并设△OAP的面积为S.
(1)S与x的函数解析式,求自变量x的取值范围.
(2)如果△OAP的面积大于1,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
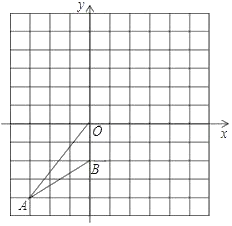
【题目】如图,已知,在平面直角坐标系中,A(﹣3,﹣4),B(0,﹣2).
(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标.
(2)判断以A,B,A1,B1为顶点的四边形的形状,请直接在答卷上填写答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
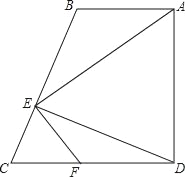
【题目】如图,在四边形ABCD中,AB∥CD,∠ADC=90°,DE⊥BC于E,连AE,FE⊥AE交CD于点F.
(1)求证:△AED∽△FEC;
(2)若AB=2![]() ,求DF的值;
,求DF的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
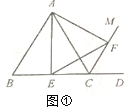
【题目】【感知】如图①,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC中点,在CM上截取CF=BE,连接AE、EF、AF.易证:△AEF是等边三角形(不需要证明).
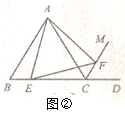
【探究】如图②,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC上一点(不与点B、C重合),在CM上截取CF=BE,连接AE、EF、AF.求证:△AEF是等边三角形.
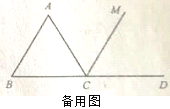
【应用】将图②中的“E是边BC上一点”改为“E是边BC延长线上一点”,其他条件不变.当四边形ACEF是轴对称图形,且AB=2时,请借助备用图,直接写出四边形ACEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com