
分析 (1)先由A、B两点的坐标求出AB=4,再根据等边三角形的定义得到AC=BC=AB=4,然后根据“m和点”的定义即可求出m=8;
(2)设点E为点A,B的“5和点”.根据“m和点”的定义可知点E在坐标轴上,再分两种情况进行讨论:①如果点E在x轴上,设E点坐标为(x,0),根据AE+BE=5列出方程|x+2|+|x-2|=5,解方程求出x的值,即可得到E点坐标;②如果点E在y轴上,设E点坐标为(0,y),根据AE+BE=5列出方程$\sqrt{{2}^{2}+{y}^{2}}+\sqrt{{2}^{2}+{y}^{2}}$=5,解方程求出y的值,即可得到E点坐标;
(3)由AB=4,可知点A,B的“m和点”的个数情况分三种情况进行讨论:①当m<4时,根据两点之间线段最短可知A,B的“m和点”没有;②当m=4时,x轴上-2与2之间的任意一个数所对应的点都是A,B的“m和点”,所以有无数个;③当m>4时,A,B的“m和点”x轴上有2个,y轴上也有2个,一共有4个.
解答 解:(1)∵A(-2,0),B(2,0),
∴AB=2-(-2)=4.
∵△ABC为等边三角形,
∴AC=BC=AB=4,
∴AC+BC=4+4=8,即m=8;
(2)设点E为点A,B的“5和点”.分两种情况:
①如果点E在x轴上,设E点坐标为(x,0).
∵AE+BE=5,
∴|x+2|+|x-2|=5,
当x≤-2时,-(x+2)-(x-2)=5,解得x=-2.5,所以E点坐标为(-2.5,0);
当-2<x≤2时,(x+2)-(x-2)=5,x无解;
当x>2时,(x+2)+(x-2)=5,解得x=2.5,所以E点坐标为(2.5,0);
②如果点E在y轴上,设E点坐标为(0,y).
∵AC+BC=5,
∴$\sqrt{{2}^{2}+{y}^{2}}+\sqrt{{2}^{2}+{y}^{2}}$=5,
∴$\sqrt{{2}^{2}+{y}^{2}}$=2.5,
两边平方,得4+y2=6.25,
解得y=±1.5.
经经验,y=±1.5都是原方程的根,
所以E点坐标为(0,1.5),(0,-1.5);
综上所述,点E在x轴上,坐标为(-2.5,0),(2.5,0);
(3)∵AB=4,
∴点A,B的“m和点”的个数情况分三种情况:
①当m<4时,A,B的“m和点”没有;
②当m=4时,A,B的“m和点”有无数个;
③当m>4时,A,B的“m和点”有4个;
所以可得点A,B的“m和点”有且只有4个,m的取值范围是m>4;
故答案为:(2)(-2.5,0),(2.5,0);(3)m>4.
点评 本题考查了勾股定理,两点间的距离公式,等边三角形的定义,同时考查学生的阅读理解能力和知识的迁移能力.正确理解A,B的“m和点”的定义是解题的前提,运用方程思想、分类讨论是解题的关键.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:选择题
| A. | x6÷x2=x3 | B. | $3{m^{-2}}=\frac{1}{{3{m^2}}}$ | C. | (a3b)2=a6b2 | D. | (a2)4=a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
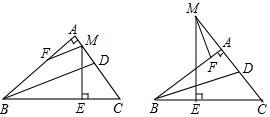
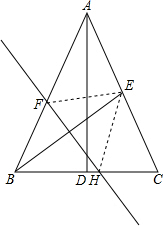 如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.
如图,在△ABC中,AB=AC,底边BC上的高AD=12,tan C=2,如果将△ABC沿直线l翻折后,点B刚好落在AC边的中点E处,直线l与边AB交于点F,与边BC交于点H,求BH的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )
在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点…则边长为8的正方形内部的整点的个数为( )| A. | 64个 | B. | 49个 | C. | 36个 | D. | 25个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
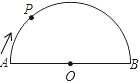 如图,在直径为AB的半圆O上有一动点P从O点出发,以相同的速度沿O-A-B-O的路线运动,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )
如图,在直径为AB的半圆O上有一动点P从O点出发,以相同的速度沿O-A-B-O的路线运动,线段OP的长度d与运动时间t之间的函数关系用图象描述大致是( )| A. | 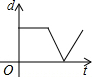 | B. | 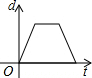 | C. | 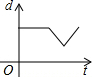 | D. | 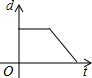 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com