
分析 先根据完全平方公式变形,设x+$\frac{1}{x}$=y,则方程化为y2-3y=0,求出y即可.
解答 解:x2+$\frac{1}{{x}^{2}}$-3(x+$\frac{1}{x}$)+2=0,
(x+$\frac{1}{x}$)2-2x$•\frac{1}{x}$-3(x+$\frac{1}{x}$)+2=0,
(x+$\frac{1}{x}$)2-3(x+$\frac{1}{x}$)=0,
设x+$\frac{1}{x}$=y,则方程化为:y2-3y=0,
解得:y=3或0,
x+$\frac{1}{x}$=3或0.
点评 本题考查了解一元二次方程的应用,能正确换元是解此题的关键,难度不是很大.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:选择题
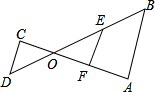 如图,若DC∥FE∥AB,则有( )
如图,若DC∥FE∥AB,则有( )| A. | $\frac{OD}{OF}$=$\frac{OC}{OE}$ | B. | $\frac{OF}{OB}$=$\frac{OA}{OC}$ | C. | $\frac{OA}{OC}$=$\frac{OD}{OB}$ | D. | $\frac{CD}{EF}$=$\frac{OD}{OE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com