练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
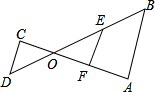
    8．如图，若DC∥FE∥AB，则有（　　）
    A．$\frac{OD}{OF}$=$\frac{OC}{OE}$B．$\frac{OF}{OB}$=$\frac{OA}{OC}$C．$\frac{OA}{OC}$=$\frac{OD}{OB}$D．$\frac{CD}{EF}$=$\frac{OD}{OE}$

    分析 根据平行线分线段成比例定理，根据题意直接列出比例等式，对比选项即可得出答案．

    解答 解：∵DC∥FE∥AB，
    ∴OD：OE=OC：OF（A错误）；
    OF：OA=OE：OB≠OB：OC（B错误）；
    OA：OC=OB：OD（C错误）；
    CD：EF=OD：OE（D正确）．
    故选D．

    点评 本题主要考查了平行线分线段成比例定理，要明确线段之间的对应关系是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

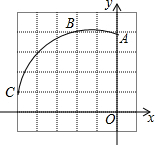    18．如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作：
    （1）利用网格确定该圆弧所在圆的圆心D点的位置，并写出点D坐标为（-1，0）；
    （2）连接AD、CD，则⊙D的半径为$\sqrt{17}$（结果保留根号），∠ADC的度数为90°；
    （3）若扇形DAC是一个圆锥的侧面展开图，则该圆锥底面半径为$\frac{\sqrt{17}}{4}$．（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．直角三角形的一条直角边长与斜边分别为8cm和10cm，则这个直角三角形斜边上的高线长为4.8 cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．若x1、x2是一元二次方程x2+ax+b=0的两个根，若x1+x2=3，则（　　）
    A．a=3B．a=-3C．b=3D．b=-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．甲口袋中装有两个相同的小球，它们的标号分别为2和7，乙口袋中装有两个相同的小球，它们的标号分别为4和5，丙口袋中装有三个相同的小球，它们的标号分别为3，8，9．从这3个口袋中各随机地取出1个小球．
    （1）求取出的3个小球的标号全是奇数的概率是多少？
    （2）若以取出的三个小球的标号分别表示三条线段的长度，请用列表或树状图法求三条线段能构成三角形的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．“晴川历历汉阳树，芳草萋萋鹦鹉洲”．武汉市在建鹦鹉州长江大桥预算总造价是9 370 000 000元人民币，“9 370 000 000”这个数用科学记数法可表示为9.37×109．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．若x3m-2-2yn-1=3是二元一次方程，则m=1，n=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

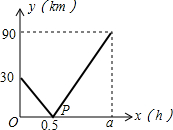    17．在一条直线上依次有A、B、C三个海岛，某海巡船从A岛出发沿直线匀速经过B岛驶向C岛，执行海巡任务，最终达到C岛．设该海巡船行驶x（h）后，与B港的距离为y（km），且y与x的函数关系如图所示，已知P点的坐标为（0.5，0），在B岛有一个不间断发射信号的信号发射台，发射的信号覆盖半径为24km，则该海巡船能接受到该信号的持续时间有0.8小时．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．解方程x4-6x2+5=0这是一个一元四次方程，通常解法：设x2=y，那么x4=y2，于是原方程可变为y2-6y+5=0，解得：y1=1，y2=5．当y=1时，x2=1，∴x=±1；当y=5时，x2=5，∴x=±$\sqrt{5}$．所以原方程有四个根：x1=1，x2=-1，x3=$\sqrt{5}$，x4=-$\sqrt{5}$．仿照上例对方程x2+$\frac{1}{{x}^{2}}$-3（x+$\frac{1}{x}$）+2=0进行转化，求代数式x+$\frac{1}{x}$的值．

    查看答案和解析>>

    同步练习册答案