
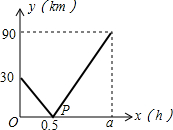
 在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经过B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),且y与x的函数关系如图所示,已知P点的坐标为(0.5,0),在B岛有一个不间断发射信号的信号发射台,发射的信号覆盖半径为24km,则该海巡船能接受到该信号的持续时间有0.8小时.
在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经过B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),且y与x的函数关系如图所示,已知P点的坐标为(0.5,0),在B岛有一个不间断发射信号的信号发射台,发射的信号覆盖半径为24km,则该海巡船能接受到该信号的持续时间有0.8小时.  孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:选择题
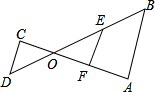 如图,若DC∥FE∥AB,则有( )
如图,若DC∥FE∥AB,则有( )| A. | $\frac{OD}{OF}$=$\frac{OC}{OE}$ | B. | $\frac{OF}{OB}$=$\frac{OA}{OC}$ | C. | $\frac{OA}{OC}$=$\frac{OD}{OB}$ | D. | $\frac{CD}{EF}$=$\frac{OD}{OE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
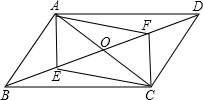 已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.
已知,如图,在平行四边形ABCD中,AC、BD相交于O点,点E、F分别为BO、DO的中点,连接AF,CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
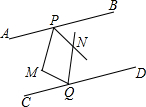 如图,M为两条平行线AB、CD之间的一点,P、Q分别在直线AB、CD上,∠BPM、∠DQM的平分线交于点N,若∠M=100°,则∠PNQ的度数为( )
如图,M为两条平行线AB、CD之间的一点,P、Q分别在直线AB、CD上,∠BPM、∠DQM的平分线交于点N,若∠M=100°,则∠PNQ的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
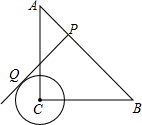 如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=4,⊙C的半径为1,点P在斜边AB上,PQ切⊙O于点Q,则切线长PQ长度的最小值为( )
如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=4,⊙C的半径为1,点P在斜边AB上,PQ切⊙O于点Q,则切线长PQ长度的最小值为( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com