
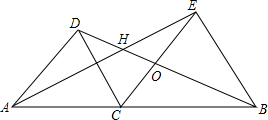
 如图,在线段AB的同侧有等边△ACD和等边△CBE,AE、DB交于H.求证:DA2=DH•DB.
如图,在线段AB的同侧有等边△ACD和等边△CBE,AE、DB交于H.求证:DA2=DH•DB. 分析 根据等边三角形的性质求出AC=CD,CE=CB,∠DCA=∠ECB=60°,∠DAC=∠ECB,求出∠ACE=∠DCB=120°,∠DAH=∠AEC,证△ACE≌△DCB,根据全等得出∠AEC=∠ABD,求出∠DAH=∠ABD,证出△ADH∽△BDA,得出比例式,即可得出答案.
解答 证明:∵△ADC和△BCE是等边三角形,
∴AC=CD,CE=CB,∠DCA=∠ECB=60°,∠DAC=∠ECB=60°,
∴∠DCE=60°,AD∥CE,
∴∠ACE=∠DCB=120°,∠DAH=∠AEC,
在△ACE和△DCB中,
$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{CE=CB}\end{array}\right.$,
∴△ACE≌△DCB,
∴∠AEC=∠ABD,
∵∠DAH=∠AEC,
∴∠DAH=∠ABD,
∵∠ADH=∠ADB,
∴△ADH∽△BDA,
∴$\frac{DA}{DH}=\frac{DB}{DA}$,
∴DA2=DH•DB.
点评 本题考查了全等三角形的性质和判定,等边三角形的性质,相似三角形的判定和性质的应用,能求出△ADH∽△BDA是解此题的关键.


科目:初中数学 来源: 题型:填空题
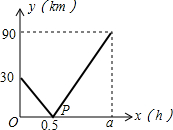 在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经过B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),且y与x的函数关系如图所示,已知P点的坐标为(0.5,0),在B岛有一个不间断发射信号的信号发射台,发射的信号覆盖半径为24km,则该海巡船能接受到该信号的持续时间有0.8小时.
在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经过B岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),且y与x的函数关系如图所示,已知P点的坐标为(0.5,0),在B岛有一个不间断发射信号的信号发射台,发射的信号覆盖半径为24km,则该海巡船能接受到该信号的持续时间有0.8小时.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-4) | B. | (-2,-8) | C. | (0,-5) | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在周长为12cm的矩形铁板上剪去一个等边三角形(这个三角形的一边是矩形的宽),则矩形的宽为$\frac{12(4-\sqrt{3})}{13}$cm时,剩下铁板的面积最大.
如图,在周长为12cm的矩形铁板上剪去一个等边三角形(这个三角形的一边是矩形的宽),则矩形的宽为$\frac{12(4-\sqrt{3})}{13}$cm时,剩下铁板的面积最大.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com