
分析 (1)根据方程x2-(2m-3)x+m2+1=0有两个实数根x1,x2,可得△=(2m-3)2-4(m2+1)≥0,求出m的取值范围即可;
(2)根据根与系数的关系得到x1+x2=2m-3,x1•x2=m2+1,进而得到y与m的函数关系式为:y=-12m+5,结合m的取值范围求出y的最小值.
解答 解:(1)∵方程x2-(2m-3)x+m2+1=0有两个实数根x1,x2,
∴△≥0,
∴(2m-3)2-4(m2+1)≥0,
∴m≤$\frac{5}{12}$;
(2)∵x1+x2=2m-3,x1•x2=m2+1,
∴(x1-x2)2=(x1+x2)2-4x1x2=(2m-3)2-4(m2+1)=-12m+5,
∴求出y与m的函数关系式为:y=-12m+5,
∵由(1)知道m≤$\frac{5}{12}$,
∴当m=$\frac{5}{12}$,y有最小值为0.
点评 本题主要考查了根的判别式、根与系数的关系以及二次函数的最值的知识,解答本题的关键是根据根的判别式求出m的取值范围,此题难度不大.


科目:初中数学 来源: 题型:解答题
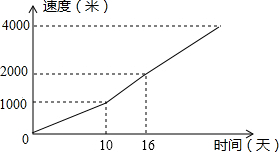 为了改善锦州市民的休闲、娱乐环境,从2013年起政府启动了小凌河水生态环境综合治理工程,有一段长为4000米的河堤需要治理,甲工程单独做了10天后,为了加快速度,决定由甲、乙两个工程队合做完成剩下的全部工程,已知工程队完成该河段河堤治理工程的进度(米)与时间(天)之间的关系如图所示:
为了改善锦州市民的休闲、娱乐环境,从2013年起政府启动了小凌河水生态环境综合治理工程,有一段长为4000米的河堤需要治理,甲工程单独做了10天后,为了加快速度,决定由甲、乙两个工程队合做完成剩下的全部工程,已知工程队完成该河段河堤治理工程的进度(米)与时间(天)之间的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-3}\\{b=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
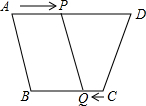 如图所示,在四边形ABCD中,AD∥CB,且AD>BC,BC=6cm,动点P,Q分别从A,C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,则2秒后四边形ABQP为平行四边形.
如图所示,在四边形ABCD中,AD∥CB,且AD>BC,BC=6cm,动点P,Q分别从A,C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动,则2秒后四边形ABQP为平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com