Question

如图，在⊙O上位于直径AB的异侧有定点C和动点P，AC=AB，点P在半圆弧AB上运动（不与A、B两点重合），过点C作直线PB的垂线CD交PB于D点．

（1）如图1，求证：△PCD∽△ABC；

（2）当点P运动到什么位置时，△PCD≌△ABC？请在图2中画出△PCD并说明理由；

（3）如图3，当点P运动到CP⊥AB时，求∠BCD的度数．

 

Answer 1

（1）见解析 （2）当PC是⊙O的直径时，△PCD≌△ABC，

（3）30°

【解析】（1）证明：∵AB是⊙O的直径，

∴∠ACB=90°，

∵PD⊥CD，

∴∠D=90°，

∴∠D=∠ACB，

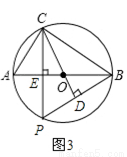
∵∠A与∠P都是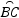对的圆周角，

∴∠A=∠P，

∴△PCD∽△ABC；

（2）【解析】

当PC是⊙O的直径时，△PCD≌△ABC，

理由：∵AB，PC是⊙O的直径，

∴∠PBC=∠ACB=90°，AB=PC，

∵∠A=∠P

∴△PCD≌△ABC；

（3）【解析】

∵∠ACB=90°，AC=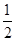AB，∴∠ABC=30°

∵OC=OB    ∴∠BCD=∠ABC=30°

（1）由AB是⊙O的直径，根据直径对的圆周角是直角，即可得∠ACB=90°，又由PD⊥CD，可得∠D=∠ACB，又由在同圆或等圆中，同弧或等弧所对的圆周角相等，即可得∠A=∠P，根据有两角对应相等的三角形相似，即可判定：△PCD∽△ABC；

（2）由△PCD∽△ABC，可知当PC=AB时，△PCD≌△ABC，利用相似比等于1的相似三角形全等即可求得；

（3）由∠ACB=90°，AC=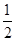AB，可求得∠ABC的度数，然后利用半径OC=OB，等角对等边，继而求得答案．