
����Ŀ��ij���ӳ��������һ������ɱ�Ϊ18Ԫ���͵��ӳ�Ʒ��Ͷ���г������������������飬�õ�ÿ��������y������������۵���x��Ԫ��֮��IJ����������£�
���۵���x��Ԫ/���� | �� | 20 | 25 | 30 | 35 | �� |
ÿ��������y������� | �� | 60 | 50 | 40 | 30 | �� |
��1�����ÿ��������y������������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2�����ÿ�µ�����z����Ԫ�������۵�x��Ԫ��֮��ĺ�����ϵʽ��
��3��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����������ʲ��ܸ���50%�����Ҹõ��ӳ���������ֲ�Ʒÿ�µ�����ɱ����ܳ���900��Ԫ����ô����������۵��۶�Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�������=�ۼ۩�����ɱ���
���𰸡�
��1���⣺��������y������������۵���x��Ԫ��֮��ĺ�����ϵʽΪ��y=kx+b��
�ѣ�20��60������30��40������y=kx+b�� ![]() ��
��
��ã� ![]() ��
��
��ÿ��������y������������۵���x��Ԫ��֮��ĺ�����ϵʽΪ��y=��2x+100
��2���⣺������ã�z=y��x��18��
=����2x+100����x��18��
=��2x2+136x��1800
��3���⣺�߳���ÿ�µ�����ɱ�������900��Ԫ��ÿ������ɱ�Ϊ18Ԫ��
��ÿ�µ�������Ϊ��С�ڵ��� ![]() =50�����
=50�����
y=��2x+100��50��
��ã�x��25��
�������������ʲ��ܸ���50%����25��x��27��
��z=��2x2+136x��1800=��2��x��34��2+512��
��ͼ�����£��Գ������z��x�����������
��x=27ʱ��z���Ϊ��404��Ԫ��
�����۵���Ϊ27Ԫʱ������ÿ�»�õ���������������Ϊ404��Ԫ
����������1���������⼴�ɵõ����ۣ�
��2����������=�������������۵���-�ɱ������������ʽ���������ϵʽ��
��3�����ݳ���ÿ�µ�����ɱ�������900��Ԫ���Լ��ɱ���18Ԫ���ó����۵��۵�ȡֵ��Χ�������ó��������
�����㾫����������Ŀ����֪����������ȷ��һ�κ����ı���ʽ�����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ������


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
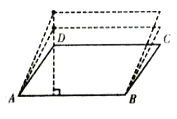
����Ŀ����ͼ��![]() �У�
�У�![]() ��ƽ�����ཻ�ڵ�D��
��ƽ�����ཻ�ڵ�D��![]() ����D��
����D��![]() ���ֱ�AB��AC�ڵ�E��F��AB=6��AC=10�����AEF���ܳ�__��
���ֱ�AB��AC�ڵ�E��F��AB=6��AC=10�����AEF���ܳ�__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���OΪֱ��AB��һ�㣬����O������OC��ʹ��AOC��60��.��һ��ֱ�����dzߵ�ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·������С�OMN��30��.
(1)��ͼ���е����dz��Ƶ�O˳ʱ����ת��ͼ�ڣ�ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC�����CON��________��
(2)��ͼ���е����dz��Ƶ�O��ÿ��10�����ٶ���˳ʱ�뷽����תһ�ܣ�����ת�Ĺ����У��ڵ�________��ʱ����MNǡ��������OCƽ�У��ڵ�________��ʱ��ֱ��ONǡ��ƽ����ǡ�AOC(ֱ��д�����)��
(3)��ͼ���е����dz��Ƶ�O˳ʱ����ת��ͼ�ۣ�ʹON�ڡ�AOC���ڲ�����̽����AOM���NOC֮���������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С���������ſ�Ƭ����Ϸ����Ƭ�Ϸֱ�д��A��B��B����Щ��Ƭ����ĸ����ȫ��ͬ�������������һ�ţ�������ĸ��Żأ����ϴ�Ⱥ��ٴ�������һ�ţ��������������Ƭ��ĸ��ͬ��С��ʤ������С��ʤ�������Ϸ��˫����ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Ϊ��ӭ�ӡ�����ڡ��ƶ��˻�ƻ��������ǻ�ƻ���IJ�����Ϣ��
������ڡ���ƻ��� | ||
�鱾��� | A�� | B�� |
���ۣ���λ��Ԫ�� | 18 | 12 |
��ע | 1���ò�����16800Ԫ����A��B����ͼ�鹲1000���� | |
��1���¾����鿴�ƻ���ʱ���֣�A��ͼ��ı����B��ͼ���۵�1.5�������˿���540Ԫ�����ͼ�飬�ܵ�������A��ͼ�������ǡ�ñȵ�������B��ͼ���������10���������A��B����ͼ��ı�ۣ�
��2�����г�����¾����������Ǹ߹��ˡ�����ڡ���ͼ�����۵�Ӱ�죬����������۷�����A��ͼ��ÿ����۽���aԪ��0��a��5�����ۣ�B��ͼ��۸䣬��ô���Ӧ��ν������ܻ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ�� y=x��1�������ύ��A��B���㣬��C��x���ϣ�����ABCΪ������������S��ABC= ![]() �����C������Ϊ�� ��
�����C�������� ��
A.����0��0 ��
B.��1�� ![]() ��0����
��0���� ![]() 1��0��
1��0��
C.���� ![]() +1��0 ��
+1��0 ��
D.������ ![]() ��1��0����
��1��0���� ![]() +1��0��
+1��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���![]() �У����ױ�
�У����ױ�![]() �ϵĸ�
�ϵĸ�![]() ��С����仯ʱ��ƽ���ı���
��С����仯ʱ��ƽ���ı���![]() �����
�����![]() Ҳ��֮�����仯�����ǵõ��������ݣ�
Ҳ��֮�����仯�����ǵõ��������ݣ�
�ױ�AB�ϵĸ�x��cm�� | 2 | 3 | 4 | 5 |
ƽ���ı���ABCD�����y(cm2) | 12 | 18 | 24 | 30 |
��1��������仯�����У��Ա�����������ֱ���ʲô��
��2��![]() ��
��![]() ֮��Ĺ�ϵʽ���Ա�ʾΪ ��
֮��Ĺ�ϵʽ���Ա�ʾΪ ��
��3���ɱ����е����ݿ��Է��֣���![]() ÿ����
ÿ����![]() ʱ��
ʱ��![]() ��α仯��
��α仯��
��4����ƽ���ı���![]() �����Ϊ
�����Ϊ![]() ����ʱ�ױ�
����ʱ�ױ�![]() �ϵĸ�Ϊ���٣�
�ϵĸ�Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺(1)�O��6�O+(![]() ��3.14)0��(
��3.14)0��(![]() )-2+(��2)3 (2)(-a)3a2+(2a4)2��a3.
)-2+(��2)3 (2)(-a)3a2+(2a4)2��a3.
(3)![]() (4)(a-2b)(a+b)��3a(a+b)
(4)(a-2b)(a+b)��3a(a+b)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com