
【题目】计算:(1)∣—6∣+(![]() —3.14)0—(
—3.14)0—(![]() )-2+(—2)3 (2)(-a)3a2+(2a4)2÷a3.
)-2+(—2)3 (2)(-a)3a2+(2a4)2÷a3.
(3)![]() (4)(a-2b)(a+b)-3a(a+b)
(4)(a-2b)(a+b)-3a(a+b)
【答案】(1)-10;(2)3a5;(3)-6a3b2+10a3b3-2a2;(4)-2a2+2b2
【解析】
(1)原式利用求绝对值,零指数幂、负指数幂法则,乘方运算法则计算即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,先算乘方,再算乘除,最后算加减,合并即可得到结果
(3)原式利用单项式乘多项式法则计算即可得到结果
(4)原式利用单项式乘多项式、多项式乘多项式法则计算即可得到结果.
(1)∣—6∣+(![]() -3.14)0—(
-3.14)0—(![]() )-2+(-2)3 =6+1-9 -8 =-10
)-2+(-2)3 =6+1-9 -8 =-10
(2)![]() =-a5+
=-a5+![]() =-a5+4a5=3a5
=-a5+4a5=3a5
(3) ![]() =-6a3b2+10a3b3-2a2
=-6a3b2+10a3b3-2a2
(4) (a+2b)(a+b)-3a(a+b)=a2+ab+2ab+2b2-3a2-3ab=-2a2+2b2


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】某电子厂商设计了一款制造成本为18元新型电子厂品,投放市场进行试销.经过调查,得到每月销售量y(万件)与销售单价x(元)之间的部分数据如下:
销售单价x(元/件) | … | 20 | 25 | 30 | 35 | … |
每月销售量y(万件) | … | 60 | 50 | 40 | 30 | … |
(1)求出每月销售量y(万件)与销售单价x(元)之间的函数关系式.
(2)求出每月的利润z(万元)与销售单x(元)之间的函数关系式.
(3)根据相关部门规定,这种电子产品的销售利润率不能高于50%,而且该电子厂制造出这种产品每月的制造成本不能超过900万元.那么并求出当销售单价定为多少元时,厂商每月能获得最大利润?最大利润是多少?(利润=售价﹣制造成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
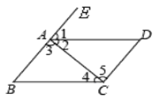
【题目】如图所示:
(1)若∠1=∠B,则_____∥_____,理由是 ;
(2)若∠3=∠5,则_____∥_____,理由是 ;
(3)若∠2=∠4,则_____∥_____,理由是 ;
(4)若∠1=∠D,则_____∥_____,理由是 ;
(5)若∠B+∠BCD=180°,_____∥_____,理由是 ;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3经过A(﹣1,0),B(3,0)两点,
(1)求二次函数解析式及对称轴方程;
(2)连接BC,交对称轴于点E,求E点坐标;
(3)在y轴上是否存在一点M,使△BCM为等腰三角形?若存在,直接写出点M的坐标;若不存在,请说明理由;
(4)在第四象限内抛物线上是否存一点H,使得四边形ACHB的面积最大?若存在,求出点H坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,∠A=70°,D、E、F分别在BC、AC、AB上,且∠1=∠2,∠3=∠4,则∠EDF等于( )

A. 70°B. 65°C. 55°D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,……,已知正方形ABCD的面积为S1为1,按上述方法所作的正方形的面积依次为S2,S3,……………,则Sn(n为正整数),那么第n个正方形的面积Sn等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l所对应的函数表达式为y=x.过点A1(0,1)作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;过点A2作y轴的垂线交直线l于点B2 , 则点B2的坐标为( )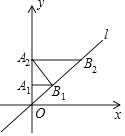
A.(1,1)
B.( ![]() ,
, ![]() )
)
C.(2,2)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com