
分析 直接利用分数的性质将原式变形,进而求出答案.
解答 解:$\frac{3}{2}$-$\frac{5}{6}$+$\frac{7}{12}$-$\frac{9}{20}$+$\frac{11}{30}$-$\frac{13}{42}$+$\frac{15}{56}$-$\frac{17}{72}$+$\frac{19}{90}$
=1+$\frac{1}{2}$-($\frac{1}{2}$+$\frac{1}{3}$)+$\frac{1}{3}$+$\frac{1}{4}$-($\frac{1}{4}$+$\frac{1}{5}$)+..+$\frac{1}{9}$+$\frac{1}{10}$
=1+$\frac{1}{10}$
=1$\frac{1}{10}$.
点评 此题主要考查了有理数的混合运算,正确利用分数的性质化简是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
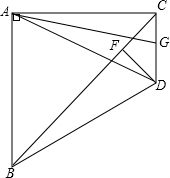 如图,△ABC是等腰直角三角形,∠BAC=90°,△ABD是等边三角形,D、C两点在直线AB同侧,连接CD交AB延长线于E,AG⊥DC于G,DF⊥CB于F.
如图,△ABC是等腰直角三角形,∠BAC=90°,△ABD是等边三角形,D、C两点在直线AB同侧,连接CD交AB延长线于E,AG⊥DC于G,DF⊥CB于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 最高气温 | 10℃ | 12℃ | 11℃ | 9℃ | 7℃ | 5℃ | 7℃ |
| 最低气温 | 2℃ | 1℃ | 0℃ | -1℃ | -4℃ | -5℃ | -5℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com