
【题目】已知![]() 与
与![]() 是两个大小不同的等腰直角三角形.
是两个大小不同的等腰直角三角形.
![]() 如图①所示,连接
如图①所示,连接![]() ,
,![]() ,试判断线段
,试判断线段![]() 和
和![]() 的数量和位置关系,并说明理由;
的数量和位置关系,并说明理由;
![]() 如图②所示,连接
如图②所示,连接![]() ,将线段
,将线段![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 到
到![]() ,连接
,连接![]() ,试判断线段
,试判断线段![]() 和
和![]() 的数量和位置关系,并说明理由.
的数量和位置关系,并说明理由.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】点A(1,n1),点B(2,n2)在一次函数y1=k1x+b1图像上:点C(3,n3),点D(4,n4)在一次函数y2=k2x+b2图像上,y1 和y2图像交点坐标是(m,n).若n4<n1<n3<n2,则下列说法:①k1>0,k2<0;②k1<0,k2>0;③1<m<3;④2<m<4,正确的是____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
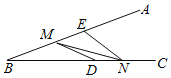
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,灯杆AB与墙MN的距离为18米,小丽在离灯杆(底部)9米的D处测得其影长DE为3m,设小丽身高为1.6m.
(1)求灯杆AB的高度;
(2)小丽再向墙走7米,她的影子能否完全落在地面上?若能,求此时的影长;若不能,求落在墙上的影长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知正方形ABCD,E是AD上一点,F是BC上一点,G是AB上一点,H是CD上一点,线段EF、GH交于点O,∠EOH=∠C,求证:EF=GH;
(2)如图2,若将“正方形ABCD”改为“菱形ABCD”,其他条件不变,探索线段EF与线段GH的关系并加以证明;
(3)如图3,若将“正方形ABCD”改为“矩形ABCD”,且AD=mAB,其他条件不变,探索线段EF与线段GH的关系并加以证明;

附加题:根据前面的探究,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题,画出图形,并证明,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师提出这样一个问题:“已知![]() ,同学们只用一块三角板可以画出它的角平分线吗?”聪明的小阳经过思考设计了如下方案(如图):
,同学们只用一块三角板可以画出它的角平分线吗?”聪明的小阳经过思考设计了如下方案(如图):
(1)在角的两边OM、ON上分别取OA=OB;
(2)过点A作DA⊥OM于点A,交ON于点D;过点B作EB⊥ON于点B,交OM于点E,AD、BE交于点C;
(3)作射线OC.
小阳接着解释说:“此时,△OAC≌△OBC,所以射线OC为∠MON的平分线。”小阳的方案中,△OAC≌△OBC的依据是( )

A.SASB.ASAC.HLD.AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成相应任务:



(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是 命题(填“真”或“假”).
(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.
(3)小颖经过探究又提出了一个新的命题:“若![]() ,
,![]() ,
,![]() , , ,则四边形
, , ,则四边形![]() ≌四边形
≌四边形![]() ”请在横线上填写两个关于“角”的条件,使该命题为真命题.
”请在横线上填写两个关于“角”的条件,使该命题为真命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=3,M为边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加![]() 场比赛,其中
场比赛,其中![]() 分球的命中率为
分球的命中率为![]() ,平均每场有
,平均每场有![]() 次
次![]() 分球未投中.
分球未投中.
![]() 该运动员去年的比赛中共投中多少个
该运动员去年的比赛中共投中多少个![]() 分球?
分球?
![]() 在其中的一场比赛中,该运动员
在其中的一场比赛中,该运动员![]() 分球共出手
分球共出手![]() 次,小明说,该运动员这场比赛中一定投中了
次,小明说,该运动员这场比赛中一定投中了![]() 个
个![]() 分球,你认为小明的说法正确吗?请说明理由.
分球,你认为小明的说法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com