
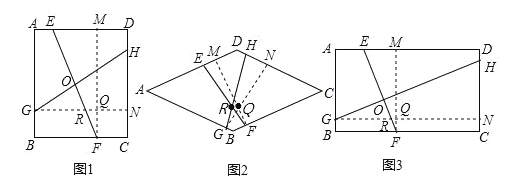
ΓΨΧβΡΩΓΩΘ®1Θ©»γΆΦ1Θ§“―÷Σ’ΐΖΫ–ΈABCDΘ§E «AD…œ“ΜΒψΘ§F «BC…œ“ΜΒψΘ§G «AB…œ“ΜΒψΘ§H «CD…œ“ΜΒψΘ§œΏΕΈEFΓΔGHΫΜ”ΎΒψOΘ§ΓœEOH=ΓœCΘ§«σ÷ΛΘΚEF=GHΘΜ
Θ®2Θ©»γΆΦ2Θ§»τΫΪΓΑ’ΐΖΫ–ΈABCDΓ±ΗΡΈΣΓΑΝβ–ΈABCDΓ±Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ§ΧΫΥςœΏΕΈEF”κœΏΕΈGHΒΡΙΊœΒ≤ΔΦ”“‘÷ΛΟςΘΜ
Θ®3Θ©»γΆΦ3Θ§»τΫΪΓΑ’ΐΖΫ–ΈABCDΓ±ΗΡΈΣΓΑΨΊ–ΈABCDΓ±Θ§«“AD=mABΘ§ΤδΥϊΧθΦΰ≤Μ±δΘ§ΧΫΥςœΏΕΈEF”κœΏΕΈGHΒΡΙΊœΒ≤ΔΦ”“‘÷ΛΟςΘΜ

ΗΫΦ”ΧβΘΚΗυΨί«ΑΟφΒΡΧΫΨΩΘ§ΡψΡήΖώΫΪ±ΨΧβΆΤΙψΒΫ“ΜΑψΒΡΤΫ––ΥΡ±Ώ–Έ«ιΩωΘΩ»τΡήΘ§–¥≥ωΆΤΙψΟϋΧβΘ§Μ≠≥ωΆΦ–ΈΘ§≤Δ÷ΛΟςΘ§»τ≤ΜΡήΘ§ΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©EF=GHΘΜ÷ΛΟςΦϊΫβΈωΘΜΘ®3Θ©![]() ΘΜ÷ΛΟςΦϊΫβΈωΘΜ
ΘΜ÷ΛΟςΦϊΫβΈωΘΜ
ΗΫΦ”ΧβΘΚΡήΘΜ÷ΛΟςΦϊΫβΈωΘΜ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§“Ή÷ΛΓςGNHΓ’ΓςFMEΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…÷ΛΒΟΫα¬έΘΜΘ®2Θ©EF=GHΘ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§÷ΛΟςΓςGNHΓ’ΓςFMEΘ§Θ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…÷ΛΒΟΫα¬έΘΜΘ®3Θ©ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§÷ΛΟςΓςGNHΓΉΓςFMEΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…÷ΛΒΟΫα¬έΘΜΗΫΦ”ΧβΘΚ»γΆΦΘ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§÷ΛΟςΓςGNHΓΉΓςFMEΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΦΑΘ®3Θ©ΒΡΫα¬έΦ¥Ω…«σΫβ.
Θ®1Θ©»γΆΦ1Θ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§
‘ρFM=GN=AD=BCΘ§«“GNΓΆFMΘ§…ηΥϋΟ«ΒΡ¥ΙΉψΈΣQΘ§…ηEFΓΔGNΫΜ”ΎR
ΓΏΓœGOF=ΓœA=90ΓψΘ§
ΓύΓœOGR=90Γψ©¹ΓœGRO=90Γψ©¹ΓœQRF=ΓœOFMΘ°
ΓΏΓœGNH=ΓœFME=90ΓψΘ§FM=GNΘ§
ΓύΓςGNHΓ’ΓςFMEΘ°
ΓύEF=GHΘ°
Θ®2Θ©»γΆΦ2Θ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§
‘ΎΥΡ±Ώ–ΈMQND÷–Θ§ΓœQMD=ΓœQND=90Γψ
ΓύΓœADC+ΓœMQN=180ΓψΘ°
ΓύΓœMQN=ΓœA=ΓœGOFΘ°
ΓΏΓœORG=ΓœQRFΘ§
ΓύΓœHGN=ΓœEFMΘ°
ΓΏΓœA=ΓœCΘ§AB=BCΘ§
ΓύFM=ABsinA=BCsinC=GNΘ°
ΓΏΓœFEM=ΓœGNH=90ΓψΘ§
ΓύΓςGNHΓ’ΓςFMEΘ°
ΓύEF=GHΘ°
Θ®3Θ©»γΆΦ3Θ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§
ΓΏΓœGOF=ΓœA=90ΓψΘ§
ΓύΓœOGR=90Γψ©¹ΓœGRO=90Γψ©¹ΓœQRF=ΓœOFMΘ°
ΓΏΓœGNH=ΓœFME=90ΓψΘ§
ΓύΓςGNHΓΉΓςFMEΘ°
Γύ![]() Θ°
Θ°
ÿGN=ADȧFM=AB,AD=mABȧ
Γύ![]() .
.
ΗΫΦ”ΧβΘΚ
“―÷ΣΤΫ––ΥΡ±Ώ–ΈABCDΘ§E «AD…œ“ΜΒψΘ§F «BC…œ“ΜΒψΘ§G «AB…œ“ΜΒψΘ§H «CD…œ“ΜΒψΘ§œΏΕΈEFΓΔGHΫΜ”ΎΒψOΘ§ΓœEOH=ΓœCΘ§AD=mABΘ§‘ρGH=mEFΘ°
÷ΛΟςΘΚ»γΆΦΘ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§
‘ΎΥΡ±Ώ–ΈMQND÷–Θ§ΓœQMD=ΓœQND=90ΓψΘ§
ΓύΓœMDN+ΓœMQN=180ΓψΘ°
ΓύΓœMQN=ΓœA=ΓœGOFΘ°
ΓΏΓœORG=ΓœQRFΘ§
ΓύΓœHGN=ΓœEFMΘ°
ΓΏΓœFME=ΓœGNH=90ΓψΘ§
ΓύΓςGNHΓΉΓςFMEΘ°
Γύ![]() =mΘ°
=mΘ°
Φ¥GH=mEFΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΗωΨΊ–ΈABCDΒΡΫœΕΧ±Ώ≥ΛΈΣ2Θ°
Θ®1Θ©»γΆΦΔΌΘ§»τ―Ί≥Λ±ΏΕ‘’έΚσΒΟΒΫΒΡΨΊ–Έ”κ‘≠ΨΊ–ΈœύΥΤΘ§«σΥϋΒΡΝμ“Μ±Ώ≥ΛΘΜ
Θ®2Θ©»γΆΦΔΎΘ§“―÷ΣΨΊ–ΈABCDΒΡΝμ“Μ±Ώ≥ΛΈΣ4Θ§Φτ»Ξ“ΜΗωΨΊ–ΈABEFΚσΘ§”ύœ¬ΒΡΨΊ–ΈEFDC”κ‘≠ΨΊ–ΈœύΥΤΘ§«σ”ύœ¬ΨΊ–ΈEFDCΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑΙζΦ“ Β––ΦΤΜ°”ΟΥ°Θ§άς––ΫΎ‘Φ”ΟΥ°Γ±ΓΑΥ° «…ζΟϋ÷°‘¥Γ±ΘΜΥ°Ή ‘¥Ϋτ»±–Έ Τ―œΨΰΘ§±ΘΜΛΥ°Ή ‘¥ΩΧ≤Μ»ίΜΚΓΘΈΣΙΡάχ –ΟώΫΎ‘Φ”ΟΥ°Θ§Ρ≥ –Ή‘ά¥Υ°ΙΪΥΨΕ‘ΒΞΈΜΚΆΗω»ΥΖ÷±π≤…»Γ“ΜΕ®¥κ ©Α¥”ΟΥ°ΝΩΖ÷ΕΈΦΤΥ°Φέ ’Ζ―Θ§ΗΟ –Ή‘ά¥Υ°ΙΪΥΨ’κΕ‘ΒΞΈΜ”ΟΥ°ΙφΕ®”ΟΥ°ΦΤΜ°ΘΚΟΩ‘¬ΒΞΈΜΦΤΜ°”ΟΥ°±ξΉΦΈΣ3000Ε÷Θ§ΦΤΜ°ΡΎ”ΟΥ°ΟΩΕ÷ ’Ζ―0.5‘ΣΘ§≥§ΦΤΜ°≤ΩΖ÷ΟΩΕ÷Α¥0.8‘Σ ’Ζ―.
Θ®1Θ©–¥≥ωΒΞΈΜΥ°Ζ―yΘ®‘ΣΘ©”κΟΩ‘¬”ΟΥ°ΝΩxΘ®Ε÷Θ©÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΚ
ΔΌ”ΟΥ°ΝΩ–Γ”ΎΒ»”Ύ3000Ε÷ ±Θ§_______________________________ΘΜ
ΔΎ”ΟΥ°ΝΩ¥σ”Ύ3000Ε÷ ±Θ§___________________________.
Θ®2Θ©Ψ≈‘¬ΖίΦΉΒΞΈΜ”ΟΥ°3200Ε÷Θ§Υ°Ζ― «_____________‘ΣΘΜ““ΒΞΈΜ”ΟΥ°2800Ε÷ΒγΘ§Υ°Ζ―_______‘Σ.
Θ®3Θ©»τ °‘¬Ζί““ΒΞΈΜΫ…Ρ…Υ°Ζ―1540‘ΣΘ§‘ρΗΟΒΞΈΜ”ΟΥ°Εύ…ΌΕ÷ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΓςABCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓςABDΈΣΒ»±Ώ»ΐΫ«–ΈΘ§Ν§Ϋ”CD

Θ®1Θ©«σΓœACDΒΡΕ» ΐ
Θ®2Θ©ΉςΓœBACΒΡΫ«ΤΫΖ÷œΏΫΜCD”ΎΒψEΘ§«σ÷ΛΘΚDEΘΫAE+CE
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§PΈΣΆΦ–ΈΆβ“ΜΒψΘ§¬ζΉψΓœCPBΘΫ60ΓψΘ§«σ÷ΛΘΚEPΤΫΖ÷ΓœCPBΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΙϊ“ΜΗωΖ÷ ΫΒΡΖ÷Ή”ΜρΖ÷ΡΗΩ…“‘“ρ ΫΖ÷ΫβΘ§«“’βΗωΖ÷ Ϋ≤ΜΩ…‘ΦΖ÷Θ§Ρ«Ο¥Έ“Ο«≥Τ’βΗωΖ÷ ΫΈΣΓΑΚΆ–≥Ζ÷ ΫΓ±Θ°
Θ®1Θ©œ¬Ν–Ζ÷ ΫΘΚΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜΔέ
ΘΜΔέ![]() ΘΜΔή
ΘΜΔή![]() Θ°Τδ÷– «ΓΑΚΆ–≥Ζ÷ ΫΓ±ΒΡ «ΓΓ ΓΓ Θ®Χν–¥–ρΚ≈Φ¥Ω…Θ©ΘΜ
Θ°Τδ÷– «ΓΑΚΆ–≥Ζ÷ ΫΓ±ΒΡ «ΓΓ ΓΓ Θ®Χν–¥–ρΚ≈Φ¥Ω…Θ©ΘΜ
Θ®2Θ©»τaΈΣ’ΐ’ϊ ΐΘ§«“![]() ΈΣΓΑΚΆ–≥Ζ÷ ΫΓ±Θ§«κ–¥≥ωaΒΡ÷ΒΓΓ ΓΓ ΘΜ
ΈΣΓΑΚΆ–≥Ζ÷ ΫΓ±Θ§«κ–¥≥ωaΒΡ÷ΒΓΓ ΓΓ ΘΜ
Θ®3Θ©‘ΎΖ÷ Ϋ‘ΥΥψ÷–Θ§Έ“Ο«“≤Μα”ΟΒΫ≈–ΕœΚΆ–≥Ζ÷ Ϋ ±Υυ–η“ΣΒΡ÷Σ ΕΘ§«κΡψ”ΟΥυ―ß÷Σ ΕΘ§Μ·Φρ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() ”κ
”κ![]() «ΝΫΗω¥σ–Γ≤ΜΆ§ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ°
«ΝΫΗω¥σ–Γ≤ΜΆ§ΒΡΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ°
![]() »γΆΦΔΌΥυ ΨΘ§Ν§Ϋ”
»γΆΦΔΌΥυ ΨΘ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ§ ‘≈–ΕœœΏΕΈ
Θ§ ‘≈–ΕœœΏΕΈ![]() ΚΆ
ΚΆ![]() ΒΡ ΐΝΩΚΆΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΒΡ ΐΝΩΚΆΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
![]() »γΆΦΔΎΥυ ΨΘ§Ν§Ϋ”
»γΆΦΔΎΥυ ΨΘ§Ν§Ϋ”![]() Θ§ΫΪœΏΕΈ
Θ§ΫΪœΏΕΈ![]() »Τ
»Τ![]() ΒψΥ≥ ±’κ–ΐΉΣ
ΒψΥ≥ ±’κ–ΐΉΣ![]() ΒΫ
ΒΫ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§ ‘≈–ΕœœΏΕΈ
Θ§ ‘≈–ΕœœΏΕΈ![]() ΚΆ
ΚΆ![]() ΒΡ ΐΝΩΚΆΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
ΒΡ ΐΝΩΚΆΈΜ÷ΟΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ,“―÷ΣΓς![]() ,Α¥“‘œ¬≤Ϋ÷ηΉςΆΦ:ΔΌΖ÷±π“‘
,Α¥“‘œ¬≤Ϋ÷ηΉςΆΦ:ΔΌΖ÷±π“‘![]() ΓΔ
ΓΔ![]() ΈΣ‘≤–ΡΘ§¥σ”Ύ
ΈΣ‘≤–ΡΘ§¥σ”Ύ![]()
![]() ΒΡ≥ΛΈΣΑκΨΕΜ≠ΜΓΘ§ΝΫΜΓΫΜ”ΎΒψ
ΒΡ≥ΛΈΣΑκΨΕΜ≠ΜΓΘ§ΝΫΜΓΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() ΘΜΔΎΉς÷±œΏ
ΘΜΔΎΉς÷±œΏ![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§»τ
Θ§»τ![]() Θ§‘ρœ¬Ν–Ϋα¬έ÷–≤Μ“ΜΕ®≥…ΝΔΒΡ «Θ® Θ©
Θ§‘ρœ¬Ν–Ϋα¬έ÷–≤Μ“ΜΕ®≥…ΝΔΒΡ «Θ® Θ©
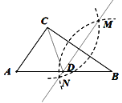
A.![]() B.Γς
B.Γς![]() «Β»±Ώ»ΐΫ«–Έ
«Β»±Ώ»ΐΫ«–Έ
C.ΒψD «ABΒΡ÷–ΒψD.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣBC=ECΘ§ΓœBCE=ΓœACDΘ§»γΙϊ÷ΜΧμΦ”“ΜΗωΧθΦΰΘ§ ΙΓςABC Γ’ ΓςDECΘ§‘ρΧμΦ”ΒΡΧθΦΰ≤ΜΡήΈΣΘ® Θ©
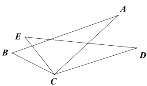
A. ΓœB=ΓœE B. AC=DC C. ΓœA=ΓœD D. AB=DE
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ÷ήΡ©Θ§Άθ―©¥χΝλ–Γ≈σ”―ΆφΟΰ«ρ”ΈœΖΘΚ‘Ύ≤ΜΆΗΟςΥήΝœ¥ϋάοΉΑ”–1ΗωΑΉ…ΪΚΆ2ΗωΜΤ…ΪΒΡΤΙ≈“«ρΘ§Οΰ≥ωΝΫΗω«ρΕΦ «ΜΤ…ΪΒΡΜώ Λ.–ΓΟς“Μ¥Έ¥”¥ϋάοΟΰ≥ωΝΫΗω«ρΘΜ–ΓΗ’Ήσ ÷¥”¥ϋάοΟΰ≥ω“ΜΗω«ρΘ§»ΜΚσ”“ ÷Οΰ≥ω“ΜΗω«ρΘΜ–ΓΜΣ‘ρœ»¥”¥ϋάοΟΰ≥ω“ΜΗω«ρΩ¥“Μœ¬―’…ΪΘ§”÷Ζ≈ΜΊ¥ϋάοΘ§‘Ό¥”¥ϋάοΟΰ≥ω“ΜΗω«ρ.’β ±Θ§–ΓΟςΦ±ΝΥΘ§ΥΒΘΚ–ΓΗ’ΓΔ–ΓΜΣ’ΦΝΥ±ψ“ΥΘ§≤ΜΙΪΤΫΘ°Ρψ»œΈΣ»γΚΈΘ® Θ©.
A. ≤ΜΙΪΤΫΘ§–ΓΗ’ΓΔ–ΓΜΣ’Φ±ψ“ΥΝΥ B. ΙΪΤΫ C. ≤ΜΙΪΤΫΘ§–ΓΜΣ≥‘ΩςΝΥ D. ≤ΜΙΪΤΫΘ§–ΓΜΣ’Φ±ψ“ΥΝΥ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com