
【题目】“国家实行计划用水,厉行节约用水”“水是生命之源”;水资源紧缺形势严峻,保护水资源刻不容缓。为鼓励市民节约用水,某市自来水公司对单位和个人分别采取一定措施按用水量分段计水价收费,该市自来水公司针对单位用水规定用水计划:每月单位计划用水标准为3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.
(1)写出单位水费y(元)与每月用水量x(吨)之间的函数关系式:
①用水量小于等于3000吨时,_______________________________;
②用水量大于3000吨时,___________________________.
(2)九月份甲单位用水3200吨,水费是_____________元;乙单位用水2800吨电,水费_______元.
(3)若十月份乙单位缴纳水费1540元,则该单位用水多少吨?
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠C=72°,∠B=∠D=90°,E,F分别是DC,BC上的点,当△AEF的周长最小时,∠EAF的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF.其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
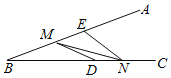
【题目】如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并完成下列问题
通过观察,发现方程:x+![]() =2+
=2+![]() 的解是:x1=2,x2=
的解是:x1=2,x2=![]() ;
;
x+![]() =3+
=3+![]() 的解是:x1=3,x2=
的解是:x1=3,x2=![]() ;
;
x+![]() =4+
=4+![]() 的解是:x1=4,x2=
的解是:x1=4,x2=![]() ;
;
……
(1)观察方程的解,猜想关于x的方程x+![]() =10+
=10+![]() 的解是 ;根据以上规律,猜想关于x的方程x+
的解是 ;根据以上规律,猜想关于x的方程x+![]() =m+
=m+![]() 的解是 ;
的解是 ;
(2)利用上述规律解关于x的方程![]() =a+
=a+![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知正方形ABCD,E是AD上一点,F是BC上一点,G是AB上一点,H是CD上一点,线段EF、GH交于点O,∠EOH=∠C,求证:EF=GH;
(2)如图2,若将“正方形ABCD”改为“菱形ABCD”,其他条件不变,探索线段EF与线段GH的关系并加以证明;
(3)如图3,若将“正方形ABCD”改为“矩形ABCD”,且AD=mAB,其他条件不变,探索线段EF与线段GH的关系并加以证明;

附加题:根据前面的探究,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题,画出图形,并证明,若不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com