
【题目】如图,△ABC和△EDC均为等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接AE,求∠EAB的度数.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
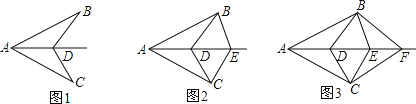
【题目】已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、BE、CE、BF、CF,图中有6对全等三角形;依此规律,第n个图形中有_____对全等三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=k(x-1)与一次函数y2=-k(x-3)的图像交于点P,其中k≠0.

(1)求点P的横坐标.
(2)点A(a,y)和点B(b,y)分别在y1和y2的图像上,若a=5,求b的值.
(3)点C(x,m)和点D(x,n)分别在y1和y2的图像上,若m-n>k,当k>0时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD交于点O,∠ABC:∠BAD=1:2,BE∥AC,CE∥BD.

(1)求tan∠DBC的值;
(2)求证:四边形OBEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2:按上述方法不断操作下去…,经过第2019次操作后得到的折痕D2018E2018,到BC的距离记为h2019:若h1=1,则h2019的值为(____)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国家实行计划用水,厉行节约用水”“水是生命之源”;水资源紧缺形势严峻,保护水资源刻不容缓。为鼓励市民节约用水,某市自来水公司对单位和个人分别采取一定措施按用水量分段计水价收费,该市自来水公司针对单位用水规定用水计划:每月单位计划用水标准为3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.
(1)写出单位水费y(元)与每月用水量x(吨)之间的函数关系式:
①用水量小于等于3000吨时,_______________________________;
②用水量大于3000吨时,___________________________.
(2)九月份甲单位用水3200吨,水费是_____________元;乙单位用水2800吨电,水费_______元.
(3)若十月份乙单位缴纳水费1540元,则该单位用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家统计局网站近日发布一组数据显示,2017年中国创新指数为196.3,比上年增长6.8%,测算结果表明,2017年,中国创新环境进一步优化,创新投入力度继续加大,创新产出持续提升,创新成效稳步增强,创新能力向高质量发展要求稳步迈进.渝北区政府在创新环境建设中,拟对城区部分路段的人行道、绿化带、排水管道等公用设施更新改造.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需20天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)市政府决定由甲、乙共同完成此项工程.若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,若工程总费用不超过143万元,则甲工程队至少工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中是“和谐分式”的是 (填写序号即可);
.其中是“和谐分式”的是 (填写序号即可);
(2)若a为正整数,且![]() 为“和谐分式”,请写出a的值 ;
为“和谐分式”,请写出a的值 ;
(3)在分式运算中,我们也会用到判断和谐分式时所需要的知识,请你用所学知识,化简![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在![]() 中,
中,![]() ,
,![]() .
.

(1)作![]() 的平分线BD,交AC于点D,作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
的平分线BD,交AC于点D,作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,判定直线AB与DE的位置关系,并对结论给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com