
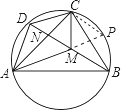
【题目】如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M在对角线BD上,且满足∠BAM=∠DAN,∠BCM=∠DCN.
求证:(1)M为BD的中点;(2)![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)要证M为BD的中点,即证BM=DM,由∠BAM=∠DAN,∠BCM=∠DCN,及圆周角的性质易证明△BAM∽△CBM,△DAM∽△CDM得出比例的乘积形式,可证明BM=DM;
(2)欲证![]() ,可以通过平行线的性质证明,需要延长AM交圆于点P,连接CP,证明PC∥BD,得出比例式,相应解决MP=CM的问题即可.
,可以通过平行线的性质证明,需要延长AM交圆于点P,连接CP,证明PC∥BD,得出比例式,相应解决MP=CM的问题即可.
试题解析:(1)根据同弧所对的圆周角相等,得∠DAN=∠DBC,∠DCN=∠DBA,
又∵∠DAN=∠BAM,∠BCM=∠DCN,
∴∠BAM=∠MBC,∠ABM=∠BCM,
∴△BAM∽△CBM,
∴![]() ,即BM2=AMCM ,①
,即BM2=AMCM ,①
又∠DCM=∠DCN+∠NCM=∠BCM+∠NCM=∠ACB=∠ADB,
∠DAM=∠MAC+∠DAN=∠MAC+∠BAM=∠BAC=∠CDM,
∴△DAM∽△CDM,
则![]() ,即DM2=AMCM ,②
,即DM2=AMCM ,②
由式①、②得:BM=DM,
即M为BD的中点;
(2)如图,延长AM交圆于点P,连接CP,
∴∠BCP=∠PAB=∠DAC=∠DBC,
∵PC∥BD,
∴![]() , ③
, ③
又∵∠MCB=∠DCA=∠ABD,∠DBC=∠PCB,
∴∠ABC=∠MCP,
而∠ABC=∠APC,
则∠APC=∠MCP,
有MP=CM,④
由式③、④得: ![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
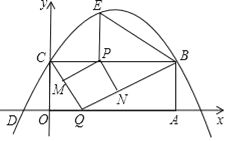
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .
(2)数轴上表示﹣12和﹣6的两点之间的距离是 .
(3)数轴上表示x和1的两点之间的距离表示为 .
(4)若x表示一个有理数,且﹣4<x<2,则|x﹣2|+|x+4|= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为3厘米,点B为⊙O外一点,OB交⊙O于点A,且AB=OA,动点P从点A出发,以π厘米/秒的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为( )秒时,直线BP与⊙O相切.

A. 1 B. 5 C. 0.5或5.5 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
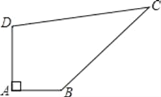
【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察下列图形与等式的关系,并填空:
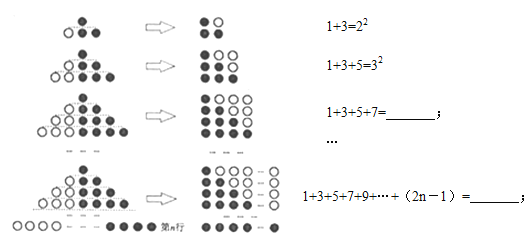
(2)利用(1)中结论,解决下列问题:
①1+3+5+…+2005= ;
②计算:101+103+105+…+199;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有理数范围内,我们定义三个数之间的新运算“![]() ”法则:a
”法则:a![]() b
b![]() c=|a+b+c|-a+b-c,例如:1
c=|a+b+c|-a+b-c,例如:1![]() 2
2![]() (-3)=|1+2+(-3)|-1+2-(-3)=4.在
(-3)=|1+2+(-3)|-1+2-(-3)=4.在![]() 这6个数中,任意取三个数作为a、b、c的值,则a
这6个数中,任意取三个数作为a、b、c的值,则a![]() b
b![]() c的最大值为___________
c的最大值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,点E是边AB上一动点(不与A,B重合),延长BA至点F,使AF=BE,连接CE,DF.
(1) 判断四边形CEFD的形状,并说明理由;
(2) 如图①,连接AC,过点E作EH⊥AC,垂足为点H.
①证明:AH=EH;
②若BE:AE=1:![]() ,求∠BCE的度数;
,求∠BCE的度数;
③如图②,连接FH,在点E的运动过程中,![]() 的值是否发生变化?若不变,求出
的值是否发生变化?若不变,求出![]() 的值;若变化,请说明理由.
的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
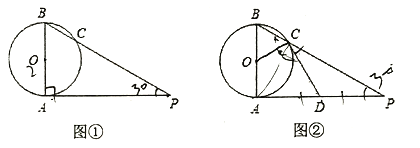
【题目】己知AB是⊙0的直径,AP是⊙0的切线,A是切点,BP与⊙0交于点C.
(1)如图①,若AB=2,∠P=30![]() ,求AP的长.(结果保留根号)
,求AP的长.(结果保留根号)
(2)如图②,若D为AP的中点,∠P=30![]() ,求证:直线CD是⊙O的切线.
,求证:直线CD是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com