
【题目】综合与探究
问题情境:
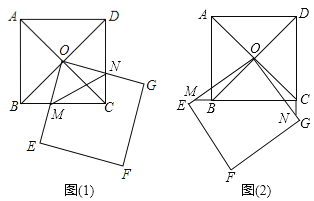
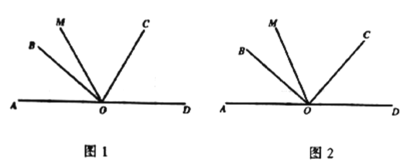
在综合实践课上,李老师让同学们根据如下问题情境,写出两个数学结论:如图(1),正方形ABCD的对角线交于点O,点O又是正方形OEFG的一个顶点(正方形OEFG的边长足够长),将正方形OEFG绕点O做旋转实验,OE与BC交于点M,OG与DC交于点N.
“兴趣小组”写出的两个数学结论是:
①S△OMC+S△ONC=![]() S正方形ABCD;
S正方形ABCD;
②BM2+CM2=2OM2.
问题解决:
(1)请你证明“兴趣小组”所写的两个结论的正确性.
类比探究:
(2)解决完“兴趣小组”的两个问题后,老师让同学们继续探究,再提出新的问题;“智慧小组“提出的问题是:如图(2),将正方形OEFG在图(1)的基础上旋转一定的角度,当OE与CB的延长线交于点M,OG与DC的延长线交于点N,则“兴趣小组”所写的两个结论是否仍然成立?请说明理由.
【答案】(1)详见解析;(2)结论①不成立,结论②成立,理由详见解析.
【解析】
(1)①利用正方形的性质判断出△BOM≌△CON,利用面积和差即可得出结论;
②先得出OM=ON,BM=CN,再用勾股定理即可得出结论;
(2)同(1)的方法即可得出结论.
解:(1)①∵正方形ABCD的对角线相交于O,
∴S△BOC=![]() S正方形ABCD,OB=OC,∠BOC=90°,∠OBM=∠OCN,
S正方形ABCD,OB=OC,∠BOC=90°,∠OBM=∠OCN,
∵四边形OEFG是正方形,
∴∠MON=90°,
∴∠BOC﹣∠MOC=∠MON﹣∠MOC,
∴∠BOM=∠COM,
∴△BOM≌△CON,
∴S△BOM=S△CON,
∴S△OMC+S△ONC=S△OMC+S△BOM=![]() S正方形ABCD;
S正方形ABCD;
②由①知,△BOM≌△CON,
∴OM=ON,BM=CN,
在Rt△MCN中,MN2=CM2+CN2=CM2+BM2,
在Rt△MON中,MN2=OM2+ON2=2OM2,
∴BM2+CM2=2OM2;
(2)结论①不成立,
理由:∵正方形ABCD的对角线相交于O,
∴S△BOC=![]() S正方形ABCD,OB=
S正方形ABCD,OB=![]() BD,OC=
BD,OC=![]() AC,AC=BD,AC⊥BD,∠ABC=∠BCD=90°,AC平分∠BCD,BD平分∠ABC,
AC,AC=BD,AC⊥BD,∠ABC=∠BCD=90°,AC平分∠BCD,BD平分∠ABC,
∴OB=OC,∠BOC=90°,∠OBC=∠OCD=45°,
∴∠OBM=∠OCN=135°,
∵四边形OEFG是正方形,
∴∠MON=90°,
∴∠BOM=∠CON,
∴△BOM≌△CON,
∴S△BOM=S△CON,
∴S△OMC﹣S△BOM=S△OMC﹣S△CON=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
∴结论①不成立;
结论②成立,理由:
如图(2)
连接MN,∵△BOM≌△CON,
∴OM=ON,BM=CN,
在Rt△MCN中,MN2=CM2+CN2=CM2+BM2,
在Rt△MON中,MN2=OM2+ON2=2OM2,
∴BM2+CM2=2OM2,
∴结论②成立.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
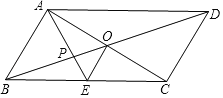
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民使用自来水按月收费,标准如下:
①若每户月用水不超过![]() ,按
,按![]() 元/
元/![]() 收费;
收费;
②若超过![]() ,但不超过
,但不超过![]() ,则超过的部分按
,则超过的部分按![]() 元/
元/![]() 收费,未超过
收费,未超过![]() 部分按①标准收费;
部分按①标准收费;
③若超过![]() ,超过的部分按
,超过的部分按![]() 元/
元/![]() 收费,未超过
收费,未超过![]() 部分按②标准收费;
部分按②标准收费;
(1)若用水![]() ,应交水费______元;(用含
,应交水费______元;(用含![]() 的式子表示)
的式子表示)
(2)小明家上个月用水![]() ,交水费
,交水费![]() 元,求
元,求![]() 的值;
的值;
(3)在(2)的条件下,小明家七、八两个月共交水费![]() 元,七月份用水
元,七月份用水![]() 超过
超过![]() ,但不足
,但不足![]() ,八月份用水
,八月份用水![]() 超过
超过![]() ,当
,当![]() 均为整数时,求
均为整数时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多边形上或内部的一点与多边形各顶点的连线,可以将多边形分割成若干个小三角形.如图,给出了四边形的三种具体分割方法,分别将四边形分割成了2个、3个、4个小三角形,这样我们就可以借助研究三角形的经验研究四边形了.
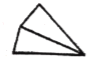
图①被分割成2个小三角形

图②被分割成3个小三角形

图③被分割成4个小三角形
(1)请按照上述三种方法分别将图中的六边形进行分割,并写出每种方法所得到的小三角形的个数:
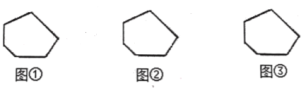
图①被分割成 个小三角形、图②被分割成 个小三角形、图③被分割成 个小三角形;
(2)如果按照上述三种分割方法分别分割![]() 边形,请写出每种方法所得到的小三角形的个数(用含
边形,请写出每种方法所得到的小三角形的个数(用含![]() 的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,
的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,![]() 边形分别可以被分割成 、 、 个小三角形.
边形分别可以被分割成 、 、 个小三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列![]() 个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
个生产、生活现象中,可用“两点之间线段最短”来解释的是( )
A.用两根钉子就可以把木条固定在墙上
B.植树时,只要选出两棵树的位置,就能确定同一行树所在的直线
C.把弯曲的公路改直,就能缩短路程
D.砌墙时,经常在两个墙角的位置分别插一根木桩拉一条直的参照线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在直线
在直线![]() 上,在直线
上,在直线![]() 的同侧,作射线
的同侧,作射线![]() 平分
平分![]() .
.
(1)如图1,若![]() ,
,![]() ,直接写出
,直接写出![]() 的度数为 ,
的度数为 ,![]() 的度数为 ;
的度数为 ;
(2)如图2,若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() 和
和![]() 互为余角且
互为余角且![]() ,
,![]() 平分
平分![]() ,试画出图形探究
,试画出图形探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com