
【题目】为了提高学校的就餐效率,巫溪中学实践小组对食堂就餐情况进行调研后发现:在单位时间内,每个窗口买走午餐的人数和因不愿长久等待而到小卖部的人数各是一个固定值,并且发现若开一个窗口,45分钟可使等待的人都能买到午餐,若同时开2个窗口,则需30分钟.还发现,若能在15分钟内买到午餐,那么在单位时间内,去小卖部就餐的人就会减少80%.在学校总人数一定且人人都要就餐的情况下,为方便学生就餐,总务处要求食堂在10分钟内卖完午餐,至少要同时开多少______个窗口.
科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间有一根绳子可看成抛物线y=0.1x2﹣0.8x+5.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为5米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面2米,求MN的长;
(3)将立柱MN的长度提升为5米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() .设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
.设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
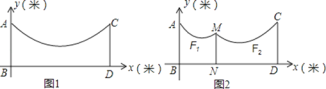
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,ΔMCN面积为2cm?
(2)是否存在某一时刻t,使四边形APNC的面积为![]() cm?若存在,求t的值,若不存在,请说明理由;
cm?若存在,求t的值,若不存在,请说明理由;
(3)当t为何值时,以A、P、M为顶点的三角形与△ABC相似?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD的垂直平分线交AD于E,交BC于F,连接BE 、DF.

(1)判断四边形BEDF的形状,并说明理由;
(2)若AB=8,AD=16,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解后面的问题.
材料:一个三位自然数![]() (百位数字为a,十位数字为b,个位数字为c),若满足a+c=b,则称这个三位数为“欢喜数”,并规定F(
(百位数字为a,十位数字为b,个位数字为c),若满足a+c=b,则称这个三位数为“欢喜数”,并规定F(![]() )=ac.如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F(374)=3×4=12.
)=ac.如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F(374)=3×4=12.
(1)对于“欢喜数![]() ”,若满足b能被9整除,求证:“欢喜数
”,若满足b能被9整除,求证:“欢喜数![]() ”能被99整除;
”能被99整除;
(2)已知有两个十位数字相同的“欢喜数”m,n(m>n),若F(m)﹣F(n)=3,求m﹣n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
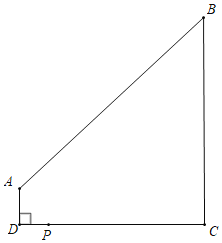
【题目】如图,AD∥BC,∠D=90°,AD=2,BC=12,DC=10,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到商场购买某个牌子的铅笔![]() 支,用了
支,用了![]() 元(
元(![]() 为整数).后来他又去商场时,发现这种牌子的铅笔降阶
为整数).后来他又去商场时,发现这种牌子的铅笔降阶![]() ,于是他比上一次多买了
,于是他比上一次多买了![]() 支铅笔,用了
支铅笔,用了![]() 元钱,那么小明两次共买了铅笔________支.
元钱,那么小明两次共买了铅笔________支.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
【1】从A、D、E、F四点中任意取一点,以所取的这一点及B、C为顶点三角形,则所画三角形是等腰三角形的概率是 ▲ ;
【2】从A、D、E、F四点中先后任意取两个不同的点,以所取的这两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表求解).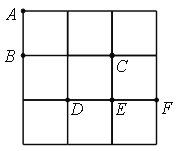
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com