
【题目】如图1,地面BD上两根等长立柱AB,CD之间有一根绳子可看成抛物线y=0.1x2﹣0.8x+5.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为5米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面2米,求MN的长;
(3)将立柱MN的长度提升为5米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() .设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
.设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
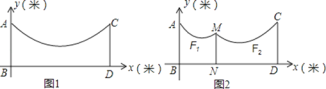
【答案】(1)![]() 米;(2)
米;(2)![]() 米;(3)2≤m≤8﹣2
米;(3)2≤m≤8﹣2![]() .
.
【解析】
(1)直接利用配方法求出二次函数最值得出答案;
(2)利用顶点式求出抛物线F1的解析式,进而得出x=5时,y的值,进而得出MN的长;
(3)根据题意得出抛物线F2的解析式,得出k的值,进而得出m的取值范围.
解:(1)∵a=0.1>0,
∴抛物线顶点为最低点,
∵y=0.1x2﹣0.8x+5=0.1(x﹣4)2+![]() ,
,
∴绳子最低点离地面的距离为:![]() 米;
米;
(2)由(1)可知,对称轴为x=4,则BD=8,
令x=0得y=5,
∴A(0,5),C(8,5),
由题意可得:抛物线F1的顶点坐标为:(4,2),
设F1的解析式为:y=a(x﹣4)2+2,
将(0,5)代入得:16a+2=5,
解得:a=![]() ,
,
∴抛物线F1为:y=![]() (x﹣4)2+2,
(x﹣4)2+2,
当x=5时,y=![]() +2=
+2=![]() ,
,
∴MN的长度为:![]() 米;
米;
(3)∵MN=DC=5,
∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,
∴F2的横坐标为:![]() (8﹣m)+m=
(8﹣m)+m=![]() m+4,
m+4,
∴抛物线F2的顶点坐标为:(![]() m+4,k),
m+4,k),
∴抛物线F2的解析式为:y=![]() (x﹣
(x﹣![]() m﹣4)2+k,
m﹣4)2+k,
把C(8,5)代入得:![]() (8﹣
(8﹣![]() m﹣4)2+k=5,
m﹣4)2+k=5,
解得:k=﹣![]() (4﹣
(4﹣![]() m)2+5,
m)2+5,
∴k=﹣![]() (m﹣8)2+5,
(m﹣8)2+5,
∴k是关于m的二次函数,
又∵由已知m<8,在对称轴的左侧,
∴k随m的增大而增大,
∴当k=2时,﹣![]() (m﹣8)2+5=2,
(m﹣8)2+5=2,
解得:m1=2,m2=14(不符合题意,舍去),
当k=3时,﹣![]() (m﹣8)2+5=3,
(m﹣8)2+5=3,
解得:m1=8﹣2![]() ,m2=8+2
,m2=8+2![]() (不符合题意,舍去),
(不符合题意,舍去),
∴m的取值范围是:2≤m≤8﹣2![]() .
.


科目:初中数学 来源: 题型:
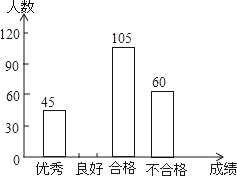
【题目】为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,每件成本8元,规定每件商品售价不低于成本,且不高于20元,经市场调查每天的销售量y(件)与每件售价x(元)满足一次函数关系,部分数据如下表:
售价x(元件) | 10 | 11 | 12 | 13 | 14 | x |
销售量y(件) | 100 | 90 | 80 | 70 |
|
|
(1)将上面的表格填充完整;
(2)设该商品每天的总利润为w元,求w与x之间的函数表达式;
(3)计算(2)中售价为多少元时,获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a满足以下三个条件:①a是整数;②关于x的一元二次方程ax2+4x﹣2=0有两个不相等的实数根;③反比例函数![]() 的图象在第二、四象限.
的图象在第二、四象限.
(1)求a的值.
(2)求一元二次方程ax2+4x﹣2=0的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平行四边形OABC中,以O为圆心,OA为半径的圆与BC相切于点B,与OC相交于点D.
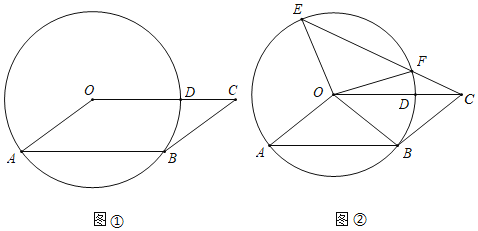
(1)求∠OAB的度数;
(2)如图②,点E在⊙O上,连接CE与⊙O交于点F,若EF=AB,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
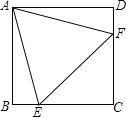
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=![]() .
.
其中正确的序号是 (把你认为正确的都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学校的就餐效率,巫溪中学实践小组对食堂就餐情况进行调研后发现:在单位时间内,每个窗口买走午餐的人数和因不愿长久等待而到小卖部的人数各是一个固定值,并且发现若开一个窗口,45分钟可使等待的人都能买到午餐,若同时开2个窗口,则需30分钟.还发现,若能在15分钟内买到午餐,那么在单位时间内,去小卖部就餐的人就会减少80%.在学校总人数一定且人人都要就餐的情况下,为方便学生就餐,总务处要求食堂在10分钟内卖完午餐,至少要同时开多少______个窗口.
查看答案和解析>>
科目:初中数学 来源: 题型:
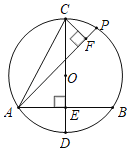
【题目】如图,在半径为2的⊙O中,弦AB⊥直径CD,垂足为E,∠ACD=30°,点P为⊙O上一动点,CF⊥AP于点F.
①弦AB的长度为_____;
②点P在⊙O上运动的过程中,线段OF长度的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com