
【题目】已知a满足以下三个条件:①a是整数;②关于x的一元二次方程ax2+4x﹣2=0有两个不相等的实数根;③反比例函数![]() 的图象在第二、四象限.
的图象在第二、四象限.
(1)求a的值.
(2)求一元二次方程ax2+4x﹣2=0的根.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+b=0(b≠0)与x2+cx+d=0都有实数根,若这两个方程有且只有一个公共根,且ab=cd,则称它们互为“同根轮换方程”.如x2-x-6=0与x2-2x-3=0互为“同根轮换方程”.
(1)若关于x的方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,求m的值;
(2)已知方程①:x2+ax+b=0和方程②:x2+2ax+![]() b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
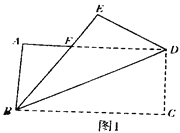
在综合实践课上,张老师让同学们以“矩形的折叠”为主题开展数学活动,张老师拿着一张矩形纸片ABCD,其中AB=acm, AD=bcm, 如图1,先沿对角线BD折叠,点C落在点E的位置,BE交AD于点F.
操作发现:
(1)“奋进”小组发现与BF的长度一定相等的线段是哪一条;
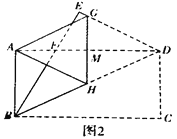
(2)如图2.“雄鹰”小组将图1再折叠一次,使点D与点A重合,得到折痕GH,GH交AD于点M,发现△DGH是等腰三角形,请你证明这个结论;
实践探究:
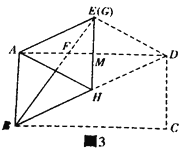
(3)“创新”小组将自己准备的矩形纸片按照(2)中“雄鹰”小组的作法操作,发现点E和点G重合,,如图3,试探究“创新”小组准备的矩形纸片中a与b满足的数量关系;
(4)”爱心”小组在其他小组的基础上提出问题:当a与b满足什么关系时,点G是DE的中点?请你直接出a与b满足的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.
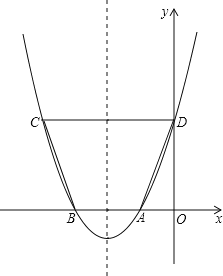
(1)求抛物线与x轴的另一个交点B的坐标;
(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式,并指出顶点E的坐标;
(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.
①当t为 秒时,△PAD的周长最小?当t为 秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)
②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN.
(1)求证:Rt△ABM≌Rt△AND
(2)线段MN与线段AD相交于T,若AT=![]() ,求
,求![]() 的值
的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com