
����Ŀ����ͼ����֪������y=ax2+bx+c��x���һ������A������Ϊ����1��0�����Գ���Ϊֱ��x=��2��
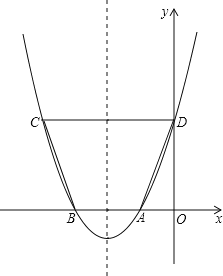
��1������������x�����һ������B�����ꣻ
��2����D����������y��Ľ��㣬��C���������ϵ���һ�㣮��֪��ABΪһ�ױߵ�����ABCD�����Ϊ9����������ߵĽ���ʽ����ָ������E�����ꣻ
��3����P�ǣ�2���������߶Գ�����һ���㣬����1����λ/����ٶȴӴ������ߵĶ���E�����˶������P�˶���ʱ��Ϊt�룮
����tΪ�� ����ʱ����PAD���ܳ���С����tΪ�� ����ʱ����PAD����ADΪ���ĵ��������Σ�������������ţ�
����P���˶������У��Ƿ����һ��P��ʹ��PAD����ADΪб�ߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡��⣺��1���������ߵ���Գ��Լ�A����1��0�����ɵ�B����3��0����
��2���������ߵĶԳ��ύCD�ڵ�M����AB�ڵ�N��
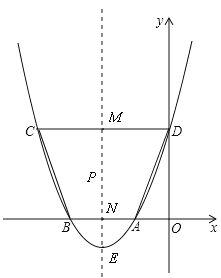
�������֪AB��CD���������ߵ���Գ��Կɵ�CD=2DM��
��MN��y�ᣬAB��CD�����ı���ODMN�Ǿ��Ρ�
��DM=ON=2����CD=2��2=4��
��A����1��0����B����3��0������AB=2��
������ABCD�����=![]() ��AB+CD��OD=9��
��AB+CD��OD=9��
��OD=3����c=3��
��A����1��0����B����3��0������y=ax2+bx+3��
![]() �����
�����![]() ��
��
��y=x2+4x+3��
��y=x2+4x+3��Ϊ����ʽΪy=��x+2��2��1����E����2����1������
��3����2�� 4��![]() ��
��![]() ��
��
�����ڡ�
�ߡ�APD=90�㣬��PMD=��PNA=90�㣬���PDM+��APN=90�㣬��DPM+��PDM=90�㡣
���PDM=��APN��
�ߡ�PMD=��ANP�����APN�ס�PDM��
��![]() ����
����![]() ��
��
��PN2��3PN+2=0�����PN=1��PN=2��
��P����2��1����2��2����
��������
������1�����������ߵ���Գ��Կɵ���������x�����һ������B��������
��2���ȸ�������ABCD�����Ϊ9������c��ֵ�������ô���ϵ�������������ߵĽ���ʽ��ת��Ϊ����ʽ����E��������
��3����������ԳƩ����·��������ɵ���PAD���ܳ���Сʱt��ֵ�����ݵ��������ε����ʿɷ�������������PAD����ADΪ���ĵ���������ʱt��ֵ��
����֤����APN�ס�PDM���������������ε��������PN��ֵ���Ӷ��õ���P��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y��ax2��bx������A(2��4)�͵�B(6��0)��
(1)����������������Ӧ�Ķ��κ����Ľ���ʽ��
(2)ֱ��д�����Ŀ��ڷ��������ꣻ
(3)��(x1��y1)��(x2��y2)���ڴ��������ϣ���x1��x2��4����y1 ________ y2(���������������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ACBE�ڽ�����O��ABƽ����CAE��CD��AB��AB��AE�ֱ��ڵ�H��D��

��1����ͼ������֤��BD=BE��
��2����ͼ������F�ǻ�AC���е㣬����BF����CD�ڵ�M����CMF=2��CBF������FO��OC������FOC�Ķ�����
��3���ڣ�2���������£�����OD����BC=4![]() ��OD=7����BF�ij���
��OD=7����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ뾶Ϊ4����O��ֱ����P��Բ������A��B������һ�㣬��APB��ƽ���߽���O�ڵ� C������AC��BC����ABC����λ�����ڵ�ֱ������O�ཻ�ڵ�E��F����EF�ij���________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��������������������a���������ڹ���x��һԪ���η���ax2+4x��2��0����������ȵ�ʵ�������۷���������![]() ��ͼ���ڵڶ��������ޣ�
��ͼ���ڵڶ��������ޣ�
��1����a��ֵ��
��2����һԪ���η���ax2+4x��2��0�ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ABΪ��O��ֱ����CΪ��O��һ�㣬CD��AB��D��AD=9��BD=4����CΪԲ�ģ�CDΪ�뾶��Բ����O�ཻ��P��Q���㣬��PQ��CD��E����PEEQ��ֵ�ǣ� )
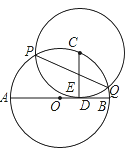
A. 24 B. 9 C. 36 D. 27
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵxoy�У���M��x����������ϣ���M��x����A��B���㣬��y����C��D���㣬��CΪ��AE���е㣬AE��y����G�㣬����A������Ϊ��-1��0����AE=4
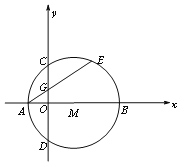
��1�����C�����ꣻ
��2������MG��BC����֤��MG��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������x�Ķ��κ���![]() ��ͼ����x�ύ�ڵ�A(1��0)�͵�B����y�ύ�ڵ�C(0��3)�������ߵĶԳ�����x�ύ�ڵ�D.
��ͼ����x�ύ�ڵ�A(1��0)�͵�B����y�ύ�ڵ�C(0��3)�������ߵĶԳ�����x�ύ�ڵ�D.
(1)����κ����ı���ʽ��
(2)��y�����Ƿ����һ��P��ʹ��PBCΪ����������.�����ڣ��������P�����ꣻ
(3)��һ����M�ӵ�A��������ÿ��1����λ���ٶ���AB�����B�˶�����һ����N�ӵ�D���Mͬʱ��������ÿ��2����λ���ٶ��������ߵĶԳ������˶�������M�� ���Bʱ����M��Nͬʱֹͣ�˶����ʵ�M��N�˶����δ�ʱ����MNB�����������������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
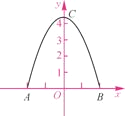
����Ŀ��ij����������һ������ˮ�ཨ����(��ͼ)�����ŵ����AB��4 m������C������Ϊ4.4 m.
(1)��AB����ֱ��Ϊx�ᣬ�����ߵĶԳ���Ϊy�ᣬ����ƽ��ֱ������ϵ����������߶�Ӧ�ĺ�������ʽ��
(2)����һ�����������������ͨ�����ţ����ﶥ������2.8 m��װ������Ϊ2.4 m����ͨ�����㣬�ж����������ܷ�˳��ͨ�����ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com