
【题目】如图①,在平行四边形OABC中,以O为圆心,OA为半径的圆与BC相切于点B,与OC相交于点D.
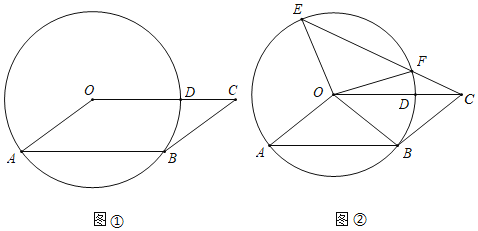
(1)求∠OAB的度数;
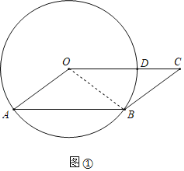
(2)如图②,点E在⊙O上,连接CE与⊙O交于点F,若EF=AB,求∠COE的度数.
【答案】(1) 45°;(2) 105°
【解析】
(1)连接OB,根据BC是圆的切线、四边形OABC是平行四边形得到△AOB是等腰直角三角形,即可求得答案;
(2)作OH⊥EC于点H,设EH=t,根据四边形OABC是平行四边形得到AB=CO=EF=2t,根据等腰直角三角形的性质可求得半径为![]() t,利用勾股定理可求得OC=2OH,从而求得∠OCE=30°,继而求得答案.
t,利用勾股定理可求得OC=2OH,从而求得∠OCE=30°,继而求得答案.
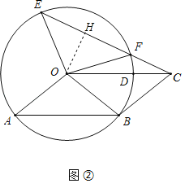
(1)如图①,连接OB,
∵BC是圆的切线,∴OB⊥BC,
∵四边形OABC是平行四边形,
∴OA∥BC,∴OB⊥OA,
∴△AOB是等腰直角三角形,
∴∠OAB=45°;
(2)如图②,过点O作OH⊥EC于点H,设EH=t,
∵OH⊥EC,
∴EF=2HE=2t,
∵四边形OABC是平行四边形,
∴AB=CO=EF=2t,
∵△AOB是等腰直角三角形,
∴OA=![]() t,
t,
则HO=![]() ,
,
∵OC=2OH,
∴∠OCE=30°,
∵HO=EH=t且OH⊥EC,
∴∠OEC=∠EOH=45°,
∴∠OEC=180°﹣∠OCE﹣∠OCE=180°﹣45°﹣30°=105°.


科目:初中数学 来源: 题型:
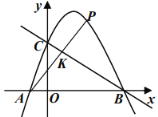
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() 为该二次函数在第一象限内的一点,连接
为该二次函数在第一象限内的一点,连接![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 的最大值为__________.
的最大值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20![]() 海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:
海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
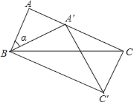
【题目】如图,在△ABC中,∠A=80°,AC=BC,以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′BC′,点A′恰好落在AC上,连接CC′,则∠ACC′=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间有一根绳子可看成抛物线y=0.1x2﹣0.8x+5.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为5米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面2米,求MN的长;
(3)将立柱MN的长度提升为5米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() .设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
.设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
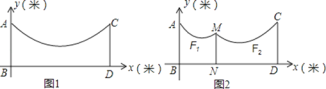
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BE平分∠ABC,CF平分∠BCD,E、F在AD上,BE与CF相交于点G,若AB=7,BC=10,则△EFG与△BCG的面积之比为( )
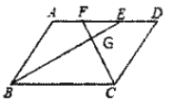
A.4:25B.49:100C.7:10D.2:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,ΔMCN面积为2cm?
(2)是否存在某一时刻t,使四边形APNC的面积为![]() cm?若存在,求t的值,若不存在,请说明理由;
cm?若存在,求t的值,若不存在,请说明理由;
(3)当t为何值时,以A、P、M为顶点的三角形与△ABC相似?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解后面的问题.
材料:一个三位自然数![]() (百位数字为a,十位数字为b,个位数字为c),若满足a+c=b,则称这个三位数为“欢喜数”,并规定F(
(百位数字为a,十位数字为b,个位数字为c),若满足a+c=b,则称这个三位数为“欢喜数”,并规定F(![]() )=ac.如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F(374)=3×4=12.
)=ac.如374,因为它的百位上数字3与个位数字4之和等于十位上的数字7,所以374是“欢喜数”,∴F(374)=3×4=12.
(1)对于“欢喜数![]() ”,若满足b能被9整除,求证:“欢喜数
”,若满足b能被9整除,求证:“欢喜数![]() ”能被99整除;
”能被99整除;
(2)已知有两个十位数字相同的“欢喜数”m,n(m>n),若F(m)﹣F(n)=3,求m﹣n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com