
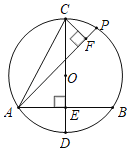
【题目】如图,在半径为2的⊙O中,弦AB⊥直径CD,垂足为E,∠ACD=30°,点P为⊙O上一动点,CF⊥AP于点F.
①弦AB的长度为_____;
②点P在⊙O上运动的过程中,线段OF长度的最小值为_____.
【答案】2![]() .
. ![]() -1
-1
【解析】
①在Rt△AOE中,解直角三角形求出AE即可解决问题.
②取AC的中点H,连接OH,OF,HF,求出OH,FH,根据OF≥FH-OH,即![]() ,由此即可解决问题.
,由此即可解决问题.
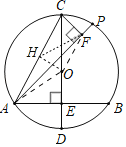
解:①如图,连接OA.
∵OA=OC=2,
∴∠OCA=∠OAC=30°,
∴∠AOE=∠OAC+∠ACO=60°,
∴AE=OAsin60°=![]() ,
,
∵OE⊥AB,
∴AE=EB=![]() ,
,
∴AB=2AE=2![]() ,
,
故答案为2![]() .
.
②取AC的中点H,连接OH,OF,HF,
∵OA=OC,AH=HC,
∴OH⊥AC,
∴∠AHO=90°,
∵∠COH=30°,
∴OH=![]() OC=1,HC=
OC=1,HC=![]() ,AC=2
,AC=2![]() ,
,
∵CF⊥AP,
∴∠AFC=90°,
∴HF=![]() AC=
AC=![]() ,
,
∴OF≥FH﹣OH,即OF≤![]() ﹣1,
﹣1,
∴OF的最小值为![]() ﹣1.
﹣1.
故答案为![]() ﹣1.
﹣1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间有一根绳子可看成抛物线y=0.1x2﹣0.8x+5.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为5米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面2米,求MN的长;
(3)将立柱MN的长度提升为5米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() .设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
.设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
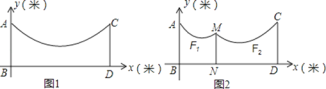
查看答案和解析>>
科目:初中数学 来源: 题型:
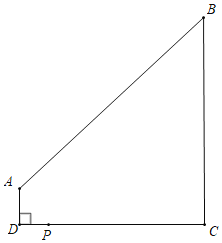
【题目】如图,AD∥BC,∠D=90°,AD=2,BC=12,DC=10,若在边DC上有点P,使△PAD与△PBC相似,则这样的点P有_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到商场购买某个牌子的铅笔![]() 支,用了
支,用了![]() 元(
元(![]() 为整数).后来他又去商场时,发现这种牌子的铅笔降阶
为整数).后来他又去商场时,发现这种牌子的铅笔降阶![]() ,于是他比上一次多买了
,于是他比上一次多买了![]() 支铅笔,用了
支铅笔,用了![]() 元钱,那么小明两次共买了铅笔________支.
元钱,那么小明两次共买了铅笔________支.
查看答案和解析>>
科目:初中数学 来源: 题型:
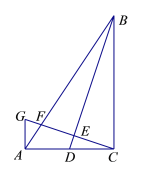
【题目】如图,在Rt△ABC中,∠ACB=90,AC=2,BC=3.点D为AC的中点,联结BD,过点C作CG⊥BD,交AC的垂线AG于点G,GC分别交BA、BD于点F、E.
(1)求GA的长;
(2)求△AFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,将△ABC绕点A顺时针旋转一定的角度![]() 得到△AED,点B、C的对应点分别是E、D.
得到△AED,点B、C的对应点分别是E、D.
(1)如图1,当点E恰好在AC上时,求∠CDE的度数;
(2)如图2,若![]() =60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.
=60°时,点F是边AC中点,求证:四边形BFDE是平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
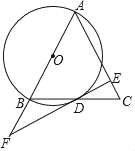
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D.过点D作EF⊥AC,垂足为E,且交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)已知AB=4,AE=3.求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
【1】从A、D、E、F四点中任意取一点,以所取的这一点及B、C为顶点三角形,则所画三角形是等腰三角形的概率是 ▲ ;
【2】从A、D、E、F四点中先后任意取两个不同的点,以所取的这两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表求解).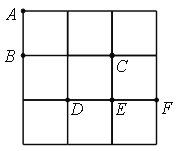
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中,有三个除颜色外其它均相同的小球,其中两个黑色,一个红色.
(1)请用表格或树状图求出:一次随机取出2个小球,颜色不同的概率.
(2)如果老师在布袋中加入若干个红色小球.然后小明通过做实验的方式猜测加入的小球数,小 明每次換出一个小球记录下慎色并放回,实验数据如下表:
实验次数 | 100 | 200 | 300 | 400 | 500 | 1000 |
摸出红球 | 78 | 147 | 228 | 304 | 373 | 752 |
请你帮小明算出老师放入了多少个红色小球.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com