
【题目】如图,正方形![]() 中,点
中,点![]() 为射线
为射线![]() 上一点,
上一点,![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,则
,则![]() ______
______
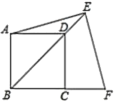
【答案】![]()
【解析】
连接AC交BD于O,作FG⊥BE于G,证出△BFG是等腰直角三角形,得出BG=FG=![]() BF=
BF=![]() ,由三角形的外角性质得出∠AED=30°,由直角三角形的性质得出OE=
,由三角形的外角性质得出∠AED=30°,由直角三角形的性质得出OE=![]() OA,求出∠FEG=60°,∠EFG=30°,进而求出OA的值,即可得出答案.
OA,求出∠FEG=60°,∠EFG=30°,进而求出OA的值,即可得出答案.
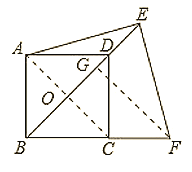
连接AC交BD于O,作FG⊥BE于G,如图所示
则∠BGF=∠EGF=90°
∵四边形ABCD是正方形
∴AC⊥BD,OA=OB=OC=OD,∠ADB=∠CBG=45°
∴△BFG是等腰直角三角形
∴BG=FG=![]() BF=
BF=![]()
∵∠ADB=∠EAD+∠AED,∠EAD=15°
∴∠AED=30°
∴OE=![]() OA
OA
∵EF⊥AE
∴∠FEG=60°
∴∠EFG=30°
∴EG=![]() FG=
FG=![]()
∴BE=BG+EG=![]()
∵OA+![]() AO=
AO=![]()
解得:OA=![]()
∴AB=![]() OA=
OA=![]()
故答案为![]()


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
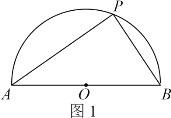
【题目】(问题发现)如图1,半圆O的直径AB=10,点P是半圆O上的一个动点,则△PAB的面积最大值是 ;
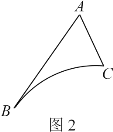
(问题探究)如图2所示,AB、AC、![]() 是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,
是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,![]() 所对的圆心角为60°.新区管委会想在
所对的圆心角为60°.新区管委会想在![]() 路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在
路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为 km;
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为 km;
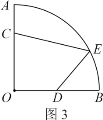
(拓展应用)如图3是某街心花园的一角,在扇形OAB中,∠AOB=90°,OA=12米,在围墙OA和OB上分别有两个入口C和D,且AC=4米,D是OB的中点,出口E在![]() 上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
①出口E设在距直线OB多远处可以使四边形CODE的面积最大?最大面积是多少?(小路宽度不计)
②已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元.
请问:在![]() 上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
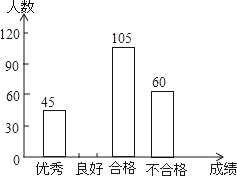
【题目】为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,关于x的方程a(1﹣x2)+2bx+c(1+x2)=0有两个相等实根,且3c=a+3b
(1)试判断△ABC的形状;
(2)求sinA+sinB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.
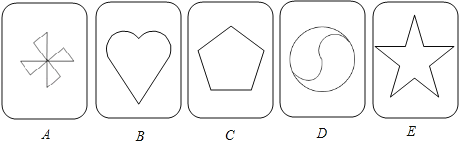
(1)从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为_____.
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
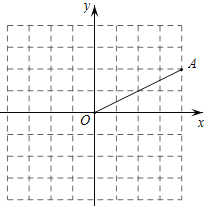
【题目】如图,点A的坐标为(4,2).将点A绕坐标原点O旋转90°后,再向左平移1个单位长度得到点A′,则过点A′的正比例函数的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,每件成本8元,规定每件商品售价不低于成本,且不高于20元,经市场调查每天的销售量y(件)与每件售价x(元)满足一次函数关系,部分数据如下表:
售价x(元件) | 10 | 11 | 12 | 13 | 14 | x |
销售量y(件) | 100 | 90 | 80 | 70 |
|
|
(1)将上面的表格填充完整;
(2)设该商品每天的总利润为w元,求w与x之间的函数表达式;
(3)计算(2)中售价为多少元时,获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学校的就餐效率,巫溪中学实践小组对食堂就餐情况进行调研后发现:在单位时间内,每个窗口买走午餐的人数和因不愿长久等待而到小卖部的人数各是一个固定值,并且发现若开一个窗口,45分钟可使等待的人都能买到午餐,若同时开2个窗口,则需30分钟.还发现,若能在15分钟内买到午餐,那么在单位时间内,去小卖部就餐的人就会减少80%.在学校总人数一定且人人都要就餐的情况下,为方便学生就餐,总务处要求食堂在10分钟内卖完午餐,至少要同时开多少______个窗口.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com