
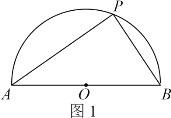
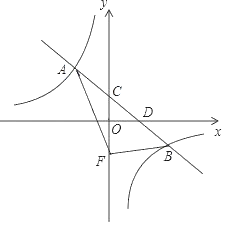
【题目】(问题发现)如图1,半圆O的直径AB=10,点P是半圆O上的一个动点,则△PAB的面积最大值是 ;
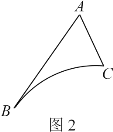
(问题探究)如图2所示,AB、AC、![]() 是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,
是某新区的三条规划路,其中AB=6km,AC=3km,∠BAC=60°,![]() 所对的圆心角为60°.新区管委会想在
所对的圆心角为60°.新区管委会想在![]() 路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在
路边建物资总站点P,在AB、AC路边分别建物资分站点E、F,即分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为 km;
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.显然,为了快捷环保和节约成本,就要使线段PE、EF、FP之和最短(各物资站点与所在道路之间的距离、路宽均忽略不计).可求得△PEF周长的最小值为 km;
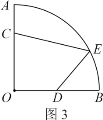
(拓展应用)如图3是某街心花园的一角,在扇形OAB中,∠AOB=90°,OA=12米,在围墙OA和OB上分别有两个入口C和D,且AC=4米,D是OB的中点,出口E在![]() 上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
上.现准备沿CE、DE从入口到出口铺设两条景观小路,在四边形CODE内种花,在剩余区域种草.
①出口E设在距直线OB多远处可以使四边形CODE的面积最大?最大面积是多少?(小路宽度不计)
②已知铺设小路CE所用的普通石材每米的造价是200元,铺设小路DE所用的景观石材每米的造价是400元.
请问:在![]() 上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
上是否存在点E,使铺设小路CE和DE的总造价最低?若存在,求出最低总造价和出口E距直线OB的距离;若不存在,请说明理由.
【答案】[问题发现] 25;[问题探究] ![]() ;[拓展应用] ①出口E设在距直线OB的7.2米处可以使四边形CODE的面积最大为60平方米,②出口E距直线OB的距离为
;[拓展应用] ①出口E设在距直线OB的7.2米处可以使四边形CODE的面积最大为60平方米,②出口E距直线OB的距离为![]() 米.
米.
【解析】
[问题发现]△PAB的底边AB一定,面积最大也就是P点到AB的距离最大,故当OP⊥AB时,![]() 时最大,值是5,再计算此时△PAB面积即可;
时最大,值是5,再计算此时△PAB面积即可;
[问题探究]先由对称将折线长转化线段长,即分别以![]() 、
、![]() 所在直线为对称轴,作出
所在直线为对称轴,作出![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,易求得:
,易求得:![]() ,而
,而![]() ,即当
,即当![]() 最小时,
最小时,![]() 可取得最小值.
可取得最小值.
[拓展应用]①四边形CODE面积=S△CDO+S△CDE′,求出S△CDE′面积最大时即可;
②先利用相似三角形将费用问题转化为CE+2DE=CE+QE,求CE+QE的最小值问题.然后利用相似三角形性质和勾股定理求解即可。
[问题发现]解:当OP⊥AB时,![]() 时最大,
时最大,![]() ,此时△APB的面积=
,此时△APB的面积=![]() ,
,
故答案为:25;
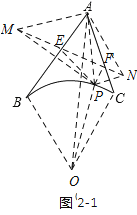
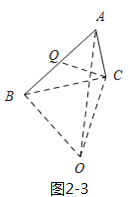
[问题探究]解:如图2-1,连接![]() ,
,![]() ,分别以
,分别以![]() 、
、![]() 所在直线为对称轴,作出
所在直线为对称轴,作出![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() 、
、![]() 、
、![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上,
为半径的圆上,
设![]() ,
,
易求得:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 当
当![]() 最小时,
最小时,![]() 可取得最小值,
可取得最小值,
![]() ,
,
![]() ,即点
,即点![]() 在
在![]() 上时,
上时,![]() 可取得最小值,如图2-2,
可取得最小值,如图2-2,
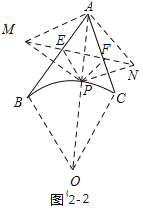
如图2-3,设![]() 的中点为
的中点为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 由勾股定理可知:
由勾股定理可知:![]() ,
,
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]()
![]() 由勾股定理可知:
由勾股定理可知:![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() 的最小值为
的最小值为![]() .
.
故答案为:![]()
[拓展应用]①如图,作OG⊥CD,垂足为G,延长OG交![]() 于点E′,则此时△CDE的面积最大.
于点E′,则此时△CDE的面积最大.
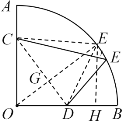
∵OA=OB=12,AC=4,点D为OB的中点,∴OC=8,OD=6,
在Rt△COD中,CD=10,OG=4.8,∴GE′=12-4.8=7.2,
∴四边形CODE面积的最大值为S△CDO+S△CDE′=![]() ×6×8+
×6×8+![]() ×10×7.2=60,
×10×7.2=60,
作E′H⊥OB,垂足为H,则E′H=![]() OE′=
OE′=![]() ×12=7.2.
×12=7.2.
答:出口E设在距直线OB的7.2米处可以使四边形CODE的面积最大为60平方米.
②铺设小路CE和DE的总造价为200CE+400DE=200(CE+2DE).
如图,连接OE,延长OB到点Q,使BQ=OB=12,连接EQ.
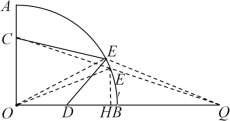
在△EOD与△QOE中,∠EOD=∠QOE,且![]() ,
,
∴△EOD∽△QOE,故QE=2DE.
于是CE+2DE=CE+QE,问题转化为求CE+QE的最小值.
连接CQ,交![]() 于点E′,此时CE+QE取得最小值为CQ,
于点E′,此时CE+QE取得最小值为CQ,
在Rt△COQ中,CO=8,OQ=24,∴CQ=8![]() ,故总造价的最小值为1600
,故总造价的最小值为1600![]() .
.
作E′H⊥OB,垂足为H,连接OE′,设E′H=x,则QH=3x,
在Rt△E′OH中,![]() ,
,
解得![]() (
(![]() 舍去),
舍去),
∴出口E距直线OB的距离为![]() 米.
米.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,2)、B(a,a+2)、C(b,0)(a>0,b>0),若AB=![]() 且∠ACB最大时,b的值为( )
且∠ACB最大时,b的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给的平面直角坐标系中按要求作图并完成填空:
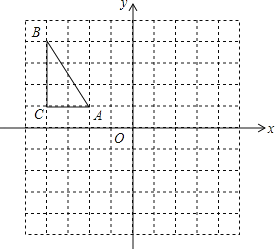
(1)作出△ABC关于原点O成中心对称的△A1B1C1,写出点A1的坐标_______.
(2)作出△A1B1C1绕点O逆时针旋转90°的△A2B2C2,写出线段C1C2的长度_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 三个顶点的坐标分别
三个顶点的坐标分别![]() .
.
(1)画出![]() ;
;
(2)以B为位似中心,将![]() 放大到原来的2倍,在右图的网格图中画出放大后的图形△
放大到原来的2倍,在右图的网格图中画出放大后的图形△![]() ;
;
(3)写出点A的对应点![]() 的坐标:___.
的坐标:___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副扑克牌中点数为“2”、“3”、“4”、“6”的四张牌背面朝上洗匀,先从中抽出1张牌,记录下牌面点数为x,再从余下的3张牌中抽出1张牌,记录下牌面点数为y.设点P的坐标为(x,y).
(1)请用表格或树状图列出点P所有可能的坐标.
(2)求点P在抛物线y=x2+x上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() 和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1)若抛物线C与直线l有交点,求a的取值范围;
(2)当a=-1,二次函数![]() 的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;
的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;
(3)若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南国际滑雪自建成以来,吸引大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离y(单位:m)与滑行时间x(单位:s)之间的关系可以近似的用二次函数来表示.
滑行时间x/s | 0 | 1 | 2 | 3 | … |
滑行距离y/m | 0 | 4 | 12 | 24 | … |
(1)根据表中数据求出二次函数的表达式.现测量出滑雪者的出发点与终点的距离大约840m,他需要多少时间才能到达终点?
(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向下平移5个单位,求平移后的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com