
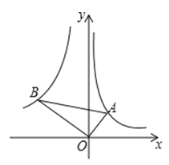
ΓΨΧβΡΩΓΩΦΟΡœΙζΦ Μ§―©Ή‘Ϋ®≥…“‘ά¥Θ§Έϋ“ΐ¥σ≈ζΜ§―©Α°ΚΟ’ΏΘ§“ΜΜ§―©’Ώ¥”…ΫΤ¬Μ§œ¬Θ§≤βΒΟΜ§––ΨύάκyΘ®ΒΞΈΜΘΚmΘ©”κΜ§–– ±ΦδxΘ®ΒΞΈΜΘΚsΘ©÷°ΦδΒΡΙΊœΒΩ…“‘ΫϋΥΤΒΡ”ΟΕΰ¥ΈΚ· ΐά¥±μ ΨΘ°
Μ§–– ±Φδx/s | 0 | 1 | 2 | 3 | Γ≠ |
Μ§––Ψύάκy/m | 0 | 4 | 12 | 24 | Γ≠ |
Θ®1Θ©ΗυΨί±μ÷– ΐΨί«σ≥ωΕΰ¥ΈΚ· ΐΒΡ±μ¥ο ΫΘ°œ÷≤βΝΩ≥ωΜ§―©’ΏΒΡ≥ωΖΔΒψ”κ÷’ΒψΒΡΨύάκ¥σ‘Φ840mΘ§Υϊ–η“ΣΕύ…Ό ±Φδ≤≈ΡήΒΫ¥ο÷’ΒψΘΩ
Θ®2Θ©ΫΪΒΟΒΫΒΡΕΰ¥ΈΚ· ΐΆΦœσ≤Ι≥δΆξ’ϊΚσΘ§œρΉσΤΫ“Τ2ΗωΒΞΈΜΘ§‘Όœρœ¬ΤΫ“Τ5ΗωΒΞΈΜΘ§«σΤΫ“ΤΚσΒΡΚ· ΐ±μ¥ο ΫΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©20sΘΜΘ®2Θ©![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ωΚ· ΐΫβΈω ΫΘ§‘Ό«σ≥ωyΘΫ840 ±xΒΡ÷ΒΦ¥Ω…ΒΟΘΜ
Θ®2Θ©ΗυΨίΓΑ…œΦ”œ¬ΦθΘ§ΉσΦ””“ΦθΓ±ΒΡ‘≠‘ρΫχ––Ϋβ¥πΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΓΏΗΟ≈ΉΈοœΏΙΐΒψΘ®0Θ§0Θ©Θ§
Γύ…η≈ΉΈοœΏΫβΈω ΫΈΣyΘΫax2+bxΘ§
ΫΪΘ®1Θ§4Θ©ΓΔΘ®2Θ§12Θ©¥ζ»κΘ§ΒΟΘΚ
![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§
Υυ“‘≈ΉΈοœΏΒΡΫβΈω ΫΈΣyΘΫ2x2+2xΘ§
Β±yΘΫ840 ±Θ§2x2+2xΘΫ840Θ§
ΫβΒΟΘΚxΘΫ20Θ®ΗΚ÷Β…α»ΞΘ©Θ§
Φ¥Υϊ–η“Σ20s≤≈ΡήΒΫ¥ο÷’ΒψΘΜ
Θ®2Θ©ΓΏyΘΫ2x2+2xΘΫ2Θ®x+![]() Θ©2©¹
Θ©2©¹![]() Θ§
Θ§
ΓύœρΉσΤΫ“Τ2ΗωΒΞΈΜΘ§‘Όœρœ¬ΤΫ“Τ5ΗωΒΞΈΜΚσΚ· ΐΫβΈω ΫΈΣyΘΫ2Θ®x+2+![]() Θ©2©¹
Θ©2©¹![]() ©¹5ΘΫ2Θ®x+
©¹5ΘΫ2Θ®x+![]() Θ©2©¹
Θ©2©¹![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Βψ![]() Θ§
Θ§![]() Ζ÷±π‘ΎΖ¥±»άΐΚ· ΐ
Ζ÷±π‘ΎΖ¥±»άΐΚ· ΐ![]()
![]() Θ§
Θ§![]()
![]() ΒΡΆΦœσ…œΘ°»τ
ΒΡΆΦœσ…œΘ°»τ![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡ÷ΒΈΣΘ® Θ©
ΒΡ÷ΒΈΣΘ® Θ©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
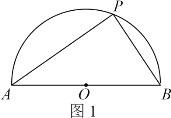
ΓΨΧβΡΩΓΩΘ®Έ ΧβΖΔœ÷Θ©»γΆΦ1Θ§Ακ‘≤OΒΡ÷±ΨΕABΘΫ10Θ§ΒψP «Ακ‘≤O…œΒΡ“ΜΗωΕ·ΒψΘ§‘ρΓςPABΒΡΟφΜΐΉν¥σ÷Β « ΘΜ
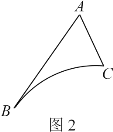
Θ®Έ ΧβΧΫΨΩΘ©»γΆΦ2Υυ ΨΘ§ABΓΔACΓΔ![]() «Ρ≥–¬«χΒΡ»ΐΧθΙφΜ°¬ΖΘ§Τδ÷–ABΘΫ6kmΘ§ACΘΫ3kmΘ§ΓœBACΘΫ60ΓψΘ§
«Ρ≥–¬«χΒΡ»ΐΧθΙφΜ°¬ΖΘ§Τδ÷–ABΘΫ6kmΘ§ACΘΫ3kmΘ§ΓœBACΘΫ60ΓψΘ§![]() ΥυΕ‘ΒΡ‘≤–ΡΫ«ΈΣ60ΓψΘ°–¬«χΙήΈ·Μαœκ‘Ύ
ΥυΕ‘ΒΡ‘≤–ΡΫ«ΈΣ60ΓψΘ°–¬«χΙήΈ·Μαœκ‘Ύ![]() ¬Ζ±ΏΫ®ΈοΉ Ήή’ΨΒψPΘ§‘ΎABΓΔAC¬Ζ±ΏΖ÷±πΫ®ΈοΉ Ζ÷’ΨΒψEΓΔFΘ§Φ¥Ζ÷±π‘Ύ
¬Ζ±ΏΫ®ΈοΉ Ήή’ΨΒψPΘ§‘ΎABΓΔAC¬Ζ±ΏΖ÷±πΫ®ΈοΉ Ζ÷’ΨΒψEΓΔFΘ§Φ¥Ζ÷±π‘Ύ![]() ΓΔœΏΕΈABΚΆAC…œ―Γ»ΓΒψPΓΔEΓΔFΘ°”…”ΎΉή’ΨΙΛΉς»Υ‘±ΟΩΧλ“ΣΫΪΈοΉ ‘ΎΗςΈοΉ ’ΨΒψΦδΑ¥PΓζEΓζFΓζPΒΡ¬ΖΨΕΫχ––‘Υ δΘ§“ρ¥ΥΘ§“Σ‘ΎΗςΈοΉ ’ΨΒψ÷°ΦδΙφΜ°Βά¬ΖPEΓΔEFΚΆFPΘ°œ‘»ΜΘ§ΈΣΝΥΩλΫίΜΖ±ΘΚΆΫΎ‘Φ≥…±ΨΘ§ΨΆ“Σ ΙœΏΕΈPEΓΔEFΓΔFP÷°ΚΆΉνΕΧΘ®ΗςΈοΉ ’ΨΒψ”κΥυ‘ΎΒά¬Ζ÷°ΦδΒΡΨύάκΓΔ¬ΖΩμΨυΚω¬‘≤ΜΦΤΘ©Θ°Ω…«σΒΟΓςPEF÷ή≥ΛΒΡΉν–Γ÷ΒΈΣ kmΘΜ
ΓΔœΏΕΈABΚΆAC…œ―Γ»ΓΒψPΓΔEΓΔFΘ°”…”ΎΉή’ΨΙΛΉς»Υ‘±ΟΩΧλ“ΣΫΪΈοΉ ‘ΎΗςΈοΉ ’ΨΒψΦδΑ¥PΓζEΓζFΓζPΒΡ¬ΖΨΕΫχ––‘Υ δΘ§“ρ¥ΥΘ§“Σ‘ΎΗςΈοΉ ’ΨΒψ÷°ΦδΙφΜ°Βά¬ΖPEΓΔEFΚΆFPΘ°œ‘»ΜΘ§ΈΣΝΥΩλΫίΜΖ±ΘΚΆΫΎ‘Φ≥…±ΨΘ§ΨΆ“Σ ΙœΏΕΈPEΓΔEFΓΔFP÷°ΚΆΉνΕΧΘ®ΗςΈοΉ ’ΨΒψ”κΥυ‘ΎΒά¬Ζ÷°ΦδΒΡΨύάκΓΔ¬ΖΩμΨυΚω¬‘≤ΜΦΤΘ©Θ°Ω…«σΒΟΓςPEF÷ή≥ΛΒΡΉν–Γ÷ΒΈΣ kmΘΜ
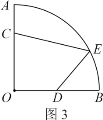
Θ®ΆΊ’Ι”Π”ΟΘ©»γΆΦ3 «Ρ≥Ϋ÷–ΡΜ®‘ΑΒΡ“ΜΫ«Θ§‘Ύ…»–ΈOAB÷–Θ§ΓœAOBΘΫ90ΓψΘ§OAΘΫ12ΟΉΘ§‘ΎΈß«ΫOAΚΆOB…œΖ÷±π”–ΝΫΗω»κΩΎCΚΆDΘ§«“ACΘΫ4ΟΉΘ§D «OBΒΡ÷–ΒψΘ§≥ωΩΎE‘Ύ![]() …œΘ°œ÷ΉΦ±Η―ΊCEΓΔDE¥”»κΩΎΒΫ≥ωΩΎΤΧ…ηΝΫΧθΨΑΙέ–Γ¬ΖΘ§‘ΎΥΡ±Ώ–ΈCODEΡΎ÷÷Μ®Θ§‘Ύ Θ”ύ«χ”ρ÷÷≤ίΘ°
…œΘ°œ÷ΉΦ±Η―ΊCEΓΔDE¥”»κΩΎΒΫ≥ωΩΎΤΧ…ηΝΫΧθΨΑΙέ–Γ¬ΖΘ§‘ΎΥΡ±Ώ–ΈCODEΡΎ÷÷Μ®Θ§‘Ύ Θ”ύ«χ”ρ÷÷≤ίΘ°
ΔΌ≥ωΩΎE…η‘ΎΨύ÷±œΏOBΕύ‘Ε¥ΠΩ…“‘ ΙΥΡ±Ώ–ΈCODEΒΡΟφΜΐΉν¥σΘΩΉν¥σΟφΜΐ «Εύ…ΌΘΩ(–Γ¬ΖΩμΕ»≤ΜΦΤ)
ΔΎ“―÷ΣΤΧ…η–Γ¬ΖCEΥυ”ΟΒΡΤ’Ά® ·≤ΡΟΩΟΉΒΡ‘λΦέ «200‘ΣΘ§ΤΧ…η–Γ¬ΖDEΥυ”ΟΒΡΨΑΙέ ·≤ΡΟΩΟΉΒΡ‘λΦέ «400‘ΣΘ°
«κΈ ΘΚ‘Ύ![]() …œ «Ζώ¥φ‘ΎΒψEΘ§ ΙΤΧ…η–Γ¬ΖCEΚΆDEΒΡΉή‘λΦέΉνΒΆΘΩ»τ¥φ‘ΎΘ§«σ≥ωΉνΒΆΉή‘λΦέΚΆ≥ωΩΎEΨύ÷±œΏOBΒΡΨύάκΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
…œ «Ζώ¥φ‘ΎΒψEΘ§ ΙΤΧ…η–Γ¬ΖCEΚΆDEΒΡΉή‘λΦέΉνΒΆΘΩ»τ¥φ‘ΎΘ§«σ≥ωΉνΒΆΉή‘λΦέΚΆ≥ωΩΎEΨύ÷±œΏOBΒΡΨύάκΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”ά≈©Μ·ΙΛ≥ß“‘ΟΩΕ÷800‘ΣΒΡΦέΗώΙΚΫχ“Μ≈ζΜ·ΙΛ‘≠ΝœΘ§Φ”ΙΛ≥…Μ·ΙΛ≤ζΤΖΫχ––œζ έΘ§“―÷ΣΟΩ1Ε÷Μ·ΙΛ‘≠ΝœΩ…“‘Φ”ΙΛ≥…Μ·ΙΛ≤ζΤΖ0.8Ε÷Θ§ΗΟ≥ß‘ΛΦΤœζ έΜ·ΙΛ≤ζΤΖ≤Μ≥§Ιΐ50Ε÷ ±ΟΩΕ÷ έΦέΈΣ1600‘ΣΘ§≥§Ιΐ50Ε÷ ±Θ§ΟΩ≥§Ιΐ1Ε÷≤ζΤΖΘ§œζ έΥυ”–ΒΡΜ·ΙΛ≤ζΤΖΟΩΕ÷ΦέΗώΨυΜαΫΒΒΆ4‘ΣΘ§…ηΗΟΜ·ΙΛ≥ß…ζ≤ζ≤Δœζ έΝΥxΕ÷Μ·ΙΛ≤ζΤΖΘ°
Θ®1Θ©”ΟxΒΡ¥ζ ΐ Ϋ±μ ΨΗΟ≥ßΙΚΫχΜ·ΙΛ‘≠ΝœΓΓ Ε÷ΘΜ
Θ®2Θ©Β±xΘΨ50 ±Θ§…ηΗΟ≥ßœζ έΆξΜ·ΙΛ≤ζΤΖΒΡΉήάϊ»σΈΣyΘ§«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©»γΙϊ“Σ«σΉήάϊ»σ≤ΜΒΆ”Ύ38400‘ΣΘ§Ρ«Ο¥ΗΟ≥ßΙΚΫχΜ·ΙΛ‘≠ΝœΒΡΕ÷ ΐ”ΠΗΟΩΊ÷Τ‘Ύ ≤Ο¥ΖΕΈßΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ RtΓςABC ÷–BC=2![]() Θ§“‘ BC ΒΡ÷–Βψ O ΈΣ‘≤–ΡΒΡΓ―O Ζ÷±π”κ ABΘ§AC œύ«–”Ύ DΘ§E ΝΫΒψΘ§
Θ§“‘ BC ΒΡ÷–Βψ O ΈΣ‘≤–ΡΒΡΓ―O Ζ÷±π”κ ABΘ§AC œύ«–”Ύ DΘ§E ΝΫΒψΘ§![]() ΒΡ≥ΛΈΣΘ® Θ©
ΒΡ≥ΛΈΣΘ® Θ©
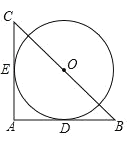
A.![]() B.
B.![]() C.Π–D.2Π–
C.Π–D.2Π–
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒ»―ϋ»ΐΫ«–ΈABCΒΡΒΉΫ«ΈΣ30ΓψΘ§“‘BCΈΣ÷±ΨΕΒΡΓ―O”κΒΉ±ΏABΫΜ”ΎΒψDΘ§ΙΐDΉςDEΓΆACΘ§¥ΙΉψΈΣEΘ°
Θ®1Θ©÷ΛΟςΘΚDEΈΣΓ―OΒΡ«–œΏΘΜ
Θ®2Θ©Ν§Ϋ”OEΘ§»τBC=4Θ§«σΓςOECΒΡΟφΜΐΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβΫώΡξ≥θ»ΐ―ß…ζΒΡ ΐ―ß―ßœΑ«ιΩωΘ§Ρ≥–ΘΕ‘…œ―ßΤΎΒΡ ΐ―ß≥…Φ®ΉςΝΥΆ≥ΦΤΖ÷ΈωΘ§Μφ÷ΤΒΟΒΫ»γœ¬ΆΦ±μΘ°«κΫαΚœΆΦ±μΥυΗχ≥ωΒΡ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
≥…Φ® | ΤΒ ΐ | ΤΒ¬ |
”≈–ψ | 45 | b |
ΝΦΚΟ | a | 0.3 |
ΚœΗώ | 105 | 0.35 |
≤ΜΚœΗώ | 60 | c |
Θ®1Θ©ΗΟ–Θ≥θ»ΐ―ß…ζΙ≤”–Εύ…Ό»ΥΘΩ
Θ®2Θ©«σ±μ÷–aΘ§bΘ§cΒΡ÷ΒΘ§≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘ°
Θ®3Θ©≥θ»ΐΘ®“ΜΘ©Αύ ΐ―ßάœ ΠΉΦ±Η¥”≥…Φ®”≈–ψΒΡΦΉΓΔ““ΓΔ±ϊΓΔΕΓΥΡΟϊΆ§―ß÷–»Έ“β≥ι»ΓΝΫΟϊΆ§―ßΉω―ßœΑΨ≠―ιΫι…ήΘ§«σ«ΓΚΟ―Γ÷–ΦΉΓΔ““ΝΫΈΜΆ§―ßΒΡΗ≈¬ Θ°
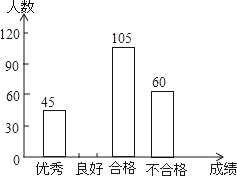
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘ΎΓςABC÷–Θ§ΓœAΘ§ΓœBΘ§ΓœCΒΡΕ‘±ΏΖ÷±π «aΘ§bΘ§cΘ§ΙΊ”ΎxΒΡΖΫ≥ΧaΘ®1©¹x2Θ©+2bx+cΘ®1+x2Θ©ΘΫ0”–ΝΫΗωœύΒ» ΒΗυΘ§«“3cΘΫa+3b
Θ®1Θ© ‘≈–ΕœΓςABCΒΡ–ΈΉ¥ΘΜ
Θ®2Θ©«σsinA+sinBΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…ΧΒξœζ έ“Μ÷÷…ΧΤΖΘ§ΟΩΦΰ≥…±Ψ8‘ΣΘ§ΙφΕ®ΟΩΦΰ…ΧΤΖ έΦέ≤ΜΒΆ”Ύ≥…±ΨΘ§«“≤ΜΗΏ”Ύ20‘ΣΘ§Ψ≠ –≥ΓΒς≤ιΟΩΧλΒΡœζ έΝΩyΘ®ΦΰΘ©”κΟΩΦΰ έΦέxΘ®‘ΣΘ©¬ζΉψ“Μ¥ΈΚ· ΐΙΊœΒΘ§≤ΩΖ÷ ΐΨί»γœ¬±μΘΚ
έΦέxΘ®‘ΣΦΰΘ© | 10 | 11 | 12 | 13 | 14 | x |
œζ έΝΩyΘ®ΦΰΘ© | 100 | 90 | 80 | 70 | ΓΓ ΓΓ | ΓΓ ΓΓ |
Θ®1Θ©ΫΪ…œΟφΒΡ±μΗώΧν≥δΆξ’ϊΘΜ
Θ®2Θ©…ηΗΟ…ΧΤΖΟΩΧλΒΡΉήάϊ»σΈΣw‘ΣΘ§«σw”κx÷°ΦδΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®3Θ©ΦΤΥψΘ®2Θ©÷– έΦέΈΣΕύ…Ό‘Σ ±Θ§ΜώΒΟΉν¥σάϊ»σΘ§Ήν¥σάϊ»σ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com