
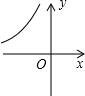
 如图,点P是双曲线y=-$\frac{{9\sqrt{3}}}{x}$(x<0)上动点,在y轴上取点Q,使得以P、Q、O为顶点的三角形是含有60°角的直角三角形,则符合条件的点Q的坐标是(0,3$\sqrt{3}$)、(0,3)、(0,12)、(0,4$\sqrt{3}$).
如图,点P是双曲线y=-$\frac{{9\sqrt{3}}}{x}$(x<0)上动点,在y轴上取点Q,使得以P、Q、O为顶点的三角形是含有60°角的直角三角形,则符合条件的点Q的坐标是(0,3$\sqrt{3}$)、(0,3)、(0,12)、(0,4$\sqrt{3}$). 分析 设P点坐标为(-a,b),a>0,可得ab=9$\sqrt{3}$;讨论:(1)若∠OQP=90°,①当∠OPQ=60°,根据含30°的直角三角形三边的关系可得b=$\sqrt{3}$a,而点P在反比例函数图象上,即可求得a与b,于是可确定Q点坐标;②当∠POQ=60°,利用同样方法可求Q点坐标;(2)若∠OPQ=90°,作PA⊥y轴于A点,①当∠POQ=60°,根据(1)可得到P点坐标,再计算AQ的长,即可得到Q点坐标;②当∠PQO=60°,计算方法与②一样.
解答 解:设点P的坐标为:(-a,b)且a>0,
则-ab=-9$\sqrt{3}$,
即ab=9$\sqrt{3}$,
(1)如图1,若∠OQP=90°,
①当∠OPQ=60°时,b=$\sqrt{3}$a,
∴$\sqrt{3}$a2=9$\sqrt{3}$,
解得:a=3,
∴b=3$\sqrt{3}$;
∴Q1的坐标为:(0,3$\sqrt{3}$);
②当∠POQ=60°时,a=$\sqrt{3}$b,
∴$\sqrt{3}$b2=9$\sqrt{3}$,
解得:b=3,
∴Q2的坐标为:(0,3);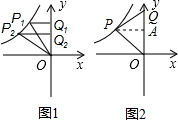
(2)如图2,若∠OPQ=90°,过点P作PA⊥y轴于点A,
①若∠POQ=60°,则a=$\sqrt{3}$b,
∴$\sqrt{3}$b2=9$\sqrt{3}$,
解得:b=3,
∴a=3$\sqrt{3}$,
∴PA=3$\sqrt{3}$,
∵∠OQP=30°,
∴AQ=PA•tan60°=9,
∴OQ=OA+AQ=12,
∴点Q的坐标为:(0,12);
②若∠PQO=60°时,则∠POQ=30°,
∴b=$\sqrt{3}$a,
∴$\sqrt{3}$a2=9$\sqrt{3}$,
解得:a=3,
∴b=3$\sqrt{3}$,
∴PA=3,
∴AQ=$\frac{PA}{tan60°}$=$\sqrt{3}$,
∴OQ=OA+AQ=4$\sqrt{3}$,
∴点Q的坐标为:(0,4$\sqrt{3}$);
综上,点Q的坐标为:(0,3$\sqrt{3}$)、(0,3)、(0,12)、(0,4$\sqrt{3}$).
故答案为:(0,3$\sqrt{3}$)、(0,3)、(0,12)、(0,4$\sqrt{3}$).
点评 本题考查了反比例函数的综合题.注意反比例函数y=$\frac{k}{x}$图象上的点满足其解析式;利用含30°的直角三角形三边的关系可简化计算;运用分类讨论的思想使解题更加完整.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
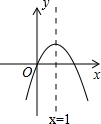 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)b>0;(2)c>0;(3)4a+2b+c>0;(4)(a+b)2<b2,其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)b>0;(2)c>0;(3)4a+2b+c>0;(4)(a+b)2<b2,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:解答题
已知方程x2﹣2x﹣8=0.解决以下问题:
(1)请 按要求分别解这个方程:①配方法;②因式分解法.
按要求分别解这个方程:①配方法;②因式分解法.
(2)①这些方法都是将解 方程转化为解 方程,以达到将方程降次的目的;
②尝试解方程:x3+2x2﹣3x=0.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等于7cm | B. | 等于10cm | ||
| C. | 不大于7cm | D. | 大于7cm而小于11cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com