
【题目】任意一个正整数都可以进行这样的分解: ![]() (
(![]() 是正整数,且
是正整数,且![]() ),正整数的所有这种分解中,如果
),正整数的所有这种分解中,如果![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是正整数的最佳分解.并规定:
是正整数的最佳分解.并规定: ![]() .例如24可以分解成1×24,2×12,3×8或4×6,因为
.例如24可以分解成1×24,2×12,3×8或4×6,因为![]() ,所以4×6是24的最佳分解,所以
,所以4×6是24的最佳分解,所以![]() .
.
(1)求![]() 的值;
的值;
(2)如果一个两位正整数, ![]() (
(![]() 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为![]() ,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为
,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为![]() ,若
,若![]() 为4752,那么我们称这个数为“最美数”,求所有“最美数”;
为4752,那么我们称这个数为“最美数”,求所有“最美数”;
(3)在(2)所得“最美数”中,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)“最美数”为48和17;(3)
;(2)“最美数”为48和17;(3)![]() .
.
【解析】试题分析:
(1)由题意可得: ![]() ,结合
,结合![]() 即可得到18的最佳分解是:
即可得到18的最佳分解是: ![]() ,从而可得:
,从而可得: ![]() ;
;
(2)由题意易到: ![]() ,
, ![]() ,由此可得:
,由此可得: ![]() 结合
结合![]() ,可得
,可得![]() ,再结合
,再结合![]() 都是自然数,且
都是自然数,且![]() 即可列出关于
即可列出关于![]() 的二元一次方程组,解方程组即可求得符合条件的
的二元一次方程组,解方程组即可求得符合条件的![]() 的值,从而可得“最美数”
的值,从而可得“最美数”![]() 的值;
的值;
(3)由(2)中所得结果结合(1)中的方法即可求得![]() 的最大值.
的最大值.
试题分析:
(1)∵![]() ,且
,且![]() ,
,
∴![]() 是
是![]() 的最佳分解,
的最佳分解,
∴![]() ;
;
(2)由题意可知: ![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,即
,即 ![]() ,
,
∵![]() 为自然数,且
为自然数,且![]() ,
,
∴![]() ,
,
解得: ![]() ,
,
∵![]() 为自然数,且
为自然数,且![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
即“最美数”为48和17;
(3)当![]() 时,∵
时,∵![]()
∴![]() ;
;
当![]() 时,∵17=1×17,
时,∵17=1×17,
∴![]() ,
,
∵![]() ,
,
∴![]() 的最大值为:
的最大值为: ![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,坐标原点O是菱形ABCD的对称中心.边AB与x轴平行,点B(1,-2),反比例函数![]() (k≠0)的图象经过A,C两点.
(k≠0)的图象经过A,C两点.
(1)求点C的坐标及反比例函数的解析式.
(2)直线BC与反比例函数图象的另一交点为E,求以O,C,E为顶点的三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年4月23日是 “世界读书日”,宜宾市某中学举行“多读书,读好书”活动,对学生的课外读书时间进行了随机问卷调查,用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题:
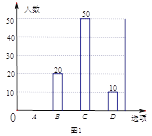
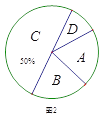
(1)本次接受问卷调查的学生共有________人,在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名学生,则该校学生课外读书时间在“A”选项的约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电厂规定:该厂家属区的每户居民一个月用电量不超过A千瓦时,那么这户居民这个月只交10元电费,如果超过A千瓦时,那么这个月除了交10元用电费外超过部分还要按每千瓦时![]() 元收费.
元收费.
(1)若某户2月份用电90千瓦时,超过规定A千瓦时,则超过部分电费为多少元?(用A表示)
(2)下表是这户居民3月、4月的用电情况和交费情况
月份 | 用电量(千瓦时) | 交电费总金额(元) |
3 | 80 | 25 |
4 | 45 | 10 |
根据上表数据,求电厂规定的A值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种商品,若购进A种商品2件和B种商品1件需45元;若购进A种商品3件和B种商品2件需70元.
(1)A、B两种商品每件的进价分别是多少元?
(2)若购进A、B两种商品共100件,总费用不超过1000元,最多能购进A种商品多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com