
【题目】某电厂规定:该厂家属区的每户居民一个月用电量不超过A千瓦时,那么这户居民这个月只交10元电费,如果超过A千瓦时,那么这个月除了交10元用电费外超过部分还要按每千瓦时![]() 元收费.
元收费.
(1)若某户2月份用电90千瓦时,超过规定A千瓦时,则超过部分电费为多少元?(用A表示)
(2)下表是这户居民3月、4月的用电情况和交费情况
月份 | 用电量(千瓦时) | 交电费总金额(元) |
3 | 80 | 25 |
4 | 45 | 10 |
根据上表数据,求电厂规定的A值为多少?
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
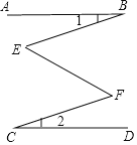
【答案】相等,理由见解析.
【解析】试题分析:分别过E、F 点作CD的平行线EM、FN,根据平行线的性质得CD∥FN∥EM∥AB,则∠3=∠1,∠4=∠5,∠1=∠6,而∠1=∠2,于是3+∠4=∠5+∠6.
试题解析:分别过E、F 点作CD的平行线EM、FN,如图
∵AB∥CD,
∴CD∥FN∥EM∥AB,
∴∠3=∠2,∠4=∠5,∠1=∠6,
而∠1=∠2,
∴∠3+∠4=∠5+∠6,
即∠BEF=∠EFC.

【题型】解答题
【结束】
26
【题目】(1)填空21-20=2( ); 22-21=2( ) ;23 -22=2( )
(2)请用字母表示第n个等式,并验证你的发现.
(3)利用(2)中你的发现,求20+21+22+23+…+22016+22017的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
①∠BOE=70°; ②OF平分∠BOD;③∠POE=∠BOF; ④∠POB=2∠DOF.
其中正确的结论有_______________(填结论前面的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意一个正整数都可以进行这样的分解: ![]() (
(![]() 是正整数,且
是正整数,且![]() ),正整数的所有这种分解中,如果
),正整数的所有这种分解中,如果![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是正整数的最佳分解.并规定:
是正整数的最佳分解.并规定: ![]() .例如24可以分解成1×24,2×12,3×8或4×6,因为
.例如24可以分解成1×24,2×12,3×8或4×6,因为![]() ,所以4×6是24的最佳分解,所以
,所以4×6是24的最佳分解,所以![]() .
.
(1)求![]() 的值;
的值;
(2)如果一个两位正整数, ![]() (
(![]() 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差记为![]() ,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为
,交换其个位上的数与十位上的数得到的新数加上原来的两位正整数所得的和记为![]() ,若
,若![]() 为4752,那么我们称这个数为“最美数”,求所有“最美数”;
为4752,那么我们称这个数为“最美数”,求所有“最美数”;
(3)在(2)所得“最美数”中,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年11月份我市某一天的最高气温是15℃,最低气温是﹣1℃,那么这一天的最高气温比最低气温高( )
A. 16℃ B. ﹣15℃ C. 14℃ D. 13℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )

A. 2个 B. 3个 C. 4个 D. 无数个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com