
����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�����оٰ�������������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 4 |
��2�� | 30��x��35 | 8 |
��3�� | 35��x��40 | 16 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |
����ͼ��������и��⣺
��1�������a��ֵ��
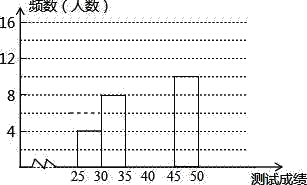
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������Գɼ�������40��Ϊ���㣬�β��Ե��������Ƕ��٣�
��4����5��10��ͬѧ�У���4����ͬѧ���ֽ���10��ͬѧƽ���ֳ�������жԿ���ϰ����4����ͬѧÿ������ˣ���С����Сǿ������ͬѧ�ܷ���ͬһ��ĸ��ʣ�
���𰸡���1��12����2����ͼ����������3��0.44����4��![]()
��������
��������������ȥ��������������ó�a��ֵ������ͳ�Ʊ�������ͳ��ͼ�������������Ȼ�����״ͼ��Ȼ��ó�����.
�⣺��1������a��ֵ�ǣ�a=50��6��8��16��10=10��
��2���������⻭ͼ���£�
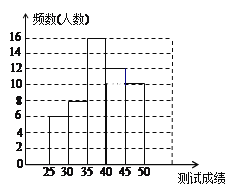
��3����A��ʾС��B��ʾСǿ��C��D��ʾ��������ͬѧ���������⻭��״ͼ���£�
![]()
����ͼ��֪����12�ֵȿ��������С����Сǿ������ͬѧ����ͬһ��������4�֣���С����Сǿ������ͬѧ����ͬһ��ĸ�����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��ѧ��ȤС��Ҫ����һ��������¥CD�ĸ߶ȣ���¥�ײ�Ϊ���⣬��2.5�ף���������ס��ÿ��߶���ȣ������֧�����1.5�ף���A�������¥������D������Ϊ60�㣬��B�������¥������E������Ϊ30�㣬AB��14�ף������¥�ĸ߶ȣ�(��ȷ��0.1�ף��ο����ݣ�![]() ��1.73)
��1.73)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ȱ�������ABC�ı߳�Ϊ5����P���߶�AB�ϣ���D���߶�BC�ϣ��ҡ�PDE�ǵȱ������Σ�
��1���������ԣ�����P���A�غ�ʱ����ͼ1����BD+BE=�� ����
��2�����̽��������P��AB�����ƶ���ʹAP=1�������������䣨��ͼ2�����Լ���BD+BE��ֵ�Ƕ��٣�
��3����չǨ�ƣ���ͼ3���ڡ�ABC�У�AB=AC����BAC=70�㣬��P���߶�AB���ӳ����ϣ���D���߶�CB���ӳ����ϣ��ڡ�PDE�У�PD=PE����DPE=70�㣬��BP=a����ֱ��д���߶�BD��BE֮���������ϵ���ú�a��ʽ�ӱ�ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��һ·����ս�Թ���Ϊ����������ҵ�ķ�չ�������µĻ�����ij��˾����A��B���ֻ�е�豸��ÿ̨B���豸�ijɱ���A���豸��![]() ������˾��Ͷ��16��Ԫ����A���豸��36��Ԫ����B���豸��������������豸��10̨�������������⣺
������˾��Ͷ��16��Ԫ����A���豸��36��Ԫ����B���豸��������������豸��10̨�������������⣺
��1��A��B�����豸ÿ̨�ijɱ��ֱ��Ƕ�����Ԫ��
��2��A��B�����豸ÿ̨���ۼ۷ֱ���6��Ԫ��10��Ԫ���ù�˾���������豸��30̨��Ϊ���õ�֧����һ��һ·����ս�Թ��룬��˾�����Ż�������һ��һ·�����ߵļ���A���豸��ԭ���ۼ�8�۳��ۣ�B���豸��ԭ���ۼ۵Ļ������Ż�10%�����豸ȫ���۳����ù�˾һ������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ�˲���ij������BC�ĸ߶ȣ�С�����ڵ������ò������A����ý����ﶥ����������30����Ȼ����ˮƽ������������ǰ����10m����D������ʱ����һб�£��¶�i=1��![]() ������б��ǰ��10����E����ý����ﶥ����������45����������ý�����BC�ĸ߶�Ϊ��������������ɴ����ţ�
������б��ǰ��10����E����ý����ﶥ����������45����������ý�����BC�ĸ߶�Ϊ��������������ɴ����ţ�

A. 5![]() +5 B. 5
+5 B. 5![]() +5 C. 5
+5 C. 5![]() +10 D. 5
+10 D. 5![]() +10
+10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���B�������ǣ�0��2��������A��ԭ��O����������x���������ƶ�����ABP����ABΪб�ߵĵ���ֱ�������Σ���A��B��P˳ʱ�뷽�����У�������A��ԭ��O�غ�ʱ���õ�����ֱ����OBC����ʱ��P���C�غϣ���
��1��BC=______����OA=2ʱ����P��������______��
��2���趯��A������Ϊ��t��0����t��0����
����֤����A���ƶ������У���ABP�Ķ���Pһ��������OC�ϣ�
���ú�t�Ĵ���ʽ��ʾ��P������Ϊ����______��______����
��3������P��y��Ĵ���PQ��QΪ���㣬��t=______ʱ����PQB����PCBȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���A��1��0����B��2��0������������ABCDEF��x������������������ÿ��ת60��Ϊ����1�Σ���ô����������ABCDEF����2017��ʱ����F�������ǣ�������

A. (2017,0) B. ��2017![]() ��
�� ![]() �� C. ��2018��
�� C. ��2018�� ![]() �� D. ��2018��0��
�� D. ��2018��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABCΪ�ȱ������Σ�EΪ����BA��һ�㣬DΪֱ��BC��һ�㣬ED.=EC.
��1������E��AB���ϣ���D��CB���ӳ�����ʱ����ͼ1������֤��AE��AC��CD��
��2������E��BA���ӳ����ϣ���D��BC��ʱ����ͼ2������д��AE��AC��CD֮���������ϵ������Ҫ֤��;
��3������E��BA���ӳ����ϣ���D��BC���ӳ�����ʱ����ͼ3������д��AE��AC��CD��������ϵ������Ҫ֤��;
��4���ڣ�1���ͣ�2���������£���AE=2��CD=6����AC= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о�������Ϊ�����ܰɣ�2018���������ܻ��������ѧУ��С��������ɷ���40������ѡ�֣��˽����ƽʱÿ���ܲ�����������λ��km����������ͳ�ƽ�����Ƴ�����Ƶ���ֲ�ֱ��ͼ�Ͳ������ı���
ÿ���ܲ�������/km | Ƶ���������� | Ƶ�� |
0��x��10 | 2 | 5% |
10��x��20 | a | m |
20��x��30 | b | 40% |
30��x��40 | 10 | 25% |
40��x��50 | 4 | n |
��1����a=������n=������
��2�����λ��10000�˲μӱ��������������������������û��ÿ���ܲ���������10��x��30 �ڵ�������
��3��Ӧ������ί��Ҫ���ִ�ÿ���ܲ���������40��x��50 �ڵ�4������ѡ�ּף��ң��������������ȡ2����Ϊ���λ����������Ա�����û���״ͼ�����б������ǡ�ó����ң������˵ĸ��ʣ�
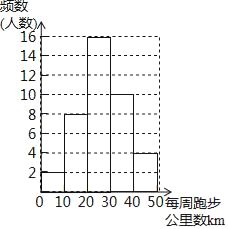
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com