
【题目】某企业有员工300人生产A种产品,平均每人每年可创造利润m万元(m为大于零的常数).为减员增效,决定从中调配x人去生产新开发的B种产品.根据评估,调配后继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54m万元.
(1)调配后企业生产A种产品的年利润为 万元,生产B种产品的年利润为 万元(用含m的代数式表示).若设调配后企业全年的总利润为y万元,则y关于x的关系式为 ;
(2)若要求调配后企业生产A种产品的年利润不少于调配前企业年利润的五分之四,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案?请设计出来,并指出其中哪种方案全年总利润最大(必要时运算过程可保留3个有效数字).
(3)企业决定将(2)中的年最大总利润(m=2)继续投资开发新产品,现有六种产品可供选择(不得重复投资同一种产品),各产品所需资金以及所获利润如下表:
产 品 | C | D | E | F | G | H |
所需资金(万元) | 200 | 348 | 240 | 288 | 240 | 500 |
年 利 润(万元) | 50 | 80 | 20 | 60 | 40 | 85 |
如果你是企业决策者,为使此项投资所获年利润不少于145万元,你可以投资开发哪些产品?请你写出两种投资方案.
【答案】(1)(300﹣x)(1+20%)m;1.54mx;y=(300﹣x)(1+20%)m+1.54mx;(2)①202人生产A产品,98人生产B产品;②201人生产A产品,99人生产B产品;③200人生产A产品,100人生产B产品;200人生产A产品,100人生产B产品总利润最大;(3)由所获年利润不少于145万元,可得投资产品为F、H或C、D、E或C、D、G或C、F、G.
【解析】
(1)调配后企业生产A种产品的年利润=生产A种产品的人数×原来平均每人每年可创造利润×(1+20%);生产B种产品的年利润=生产B种产品的人数×1.54m;总利润=调配后企业生产A种产品的年利润+生产B种产品的年利润,把相关数值代入即可;
(2)关系式为:调配后企业生产A种产品的年利润≥调配前企业年利润的五分之四,生产B种产品的年利润>调配前企业年利润的一半,把相关数值代入求得相应的取值范围,进而求得利润最大的方案即可;
(3)算出(2)的最大利润为总投资,结合获得利润可得投资开发产品种类.
解:(1)生产A种产品的人数为300﹣x,平均每人每年创造的利润为m×(1+20%)万元,
所以调配后企业生产A种产品的年利润为(300﹣x)(1+20%)m万元;
生产B种产品的人数为x,平均每人每年创造的利润为1.54m,
∴生产B种产品的年利润为1.54mx万元,调配后企业全年的总利润y=(300﹣x)(1+20%)m+1.54mx.
故答案为:(300﹣x)(1+20%)m;1.54mx;y=(300﹣x)(1+20%)m+1.54mx;
(2)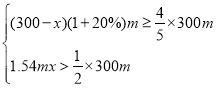 ,
,
解得![]() <x≤100,
<x≤100,
∵x为正整数,
∴x可取98,99,100.
∴①202人生产A产品,98人生产B产品;
②201人生产A产品,99人生产B产品;
③200人生产A产品,100人生产B产品;
∵y=(300﹣x)(1+20%)m+1.54mx=0.34mx+360m,
∴x越大,利润越大,
∴200人生产A产品,100人生产B产品总利润最大;
(3)当m=2,x=100时,y=788万元.由所获年利润不少于145万元,可得投资产品为F、H或C、D、E或C、D、G或C、F、G.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
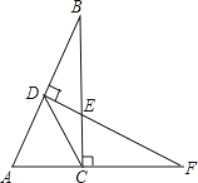
【题目】如图,CD是Rt△ABC斜边AB上的中线,过点D垂直于AB的直线交BC于E,交AC延长线于F.
求证:(1)△ADF∽△EDB;
(2)CD2=DEDF.
查看答案和解析>>
科目:初中数学 来源: 题型:
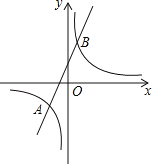
【题目】如图,直线y1=2x+1与双曲线y2=![]() 相交于A(﹣2,a)和B两点.
相交于A(﹣2,a)和B两点.
(1)求k的值;
(2)在点B上方的直线y=m与直线AB相交于点M,与双曲线y2=![]() 相交于点N,若MN=
相交于点N,若MN=![]() ,求m的值;
,求m的值;
(3)在(2)前提下,请结合图象,求不等式2x<![]() ﹣1<m﹣1的解集.
﹣1<m﹣1的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从某市近期卖出的不同面积的商 品房中随机抽取1000套进行统计,并根据结果绘出如图所示的统计图,请结合图中的信息,解析下列问题:
(1)卖出面积为110~130平方米的商品房 有___套,并在右图中补全统计图.
(2)从图中可知,卖出最多的商品房约占全部卖出的商品房的___%.

(3)假如你是房地产开发商,根据以上提供的信息,你会多建住房面积在什么范围内的住房?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
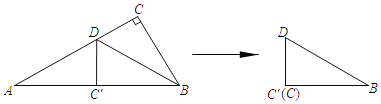
【题目】如图1,小军有一张Rt△ABC纸片,其中∠A=30°,AB=12cm.他先将该纸片沿BD折叠,使点C刚好落在斜边AB上的一点C′处.然后沿DC′剪开得到双层△BDC′(如图2).小军想把双层△BDC′沿某直线再剪开一次,使展开后的两个平面图形中其中一个是平行四边形,则他能得到的平行四边形的最大面积可为____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a、b、c为常数,且
(a、b、c为常数,且![]() )的x与y的部分对应值如下表:
)的x与y的部分对应值如下表:

有下列结论:①a>0;②4a-2b+1>0;③x=-3是关于x的一元二次方程ax2+(b-1)x+c=0的一个根;④当-3≤x≤n时,ax2+(b-1)x+c≥0.其中结论正确的有____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图.请你根据统计图回答下列问题:

(1)本次调查的学生共有 人,扇形统计图中喜欢乒乓球的学生所占的百分比为 ;
(2)请补全条形统计图(图2),并估计全校500名学生中最喜欢“足球”项目的有多少人?
(3)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com