

 ,
,
 GF·CM=3.6.
GF·CM=3.6.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源:不详 题型:单选题
 ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=
ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG= ,则梯形AECD的周长为( )
,则梯形AECD的周长为( )
| A.22 | B.23 | C.24 | D.25 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A.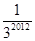 | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.对角线垂直且相等的四边形是正方形 |
| B.对角线互相垂直平分的四边形为菱形 |
| C.直角三角形的两直角边长是3和4,则斜边长是5 |
| D.顺次连接四边形各边中点得到的是矩形,则该四边形的对角线相互垂直 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.BO=DO | B.CD=AB | C.∠BAD=∠BCD | D.AC=BD |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 进行如下操作:先把点
进行如下操作:先把点 表示的数乘以
表示的数乘以 ,再把所得数对应的点向右平移1个单位,得到点
,再把所得数对应的点向右平移1个单位,得到点 的对应点
的对应点 .点
.点 在数轴上,对线段
在数轴上,对线段 上的每个点进行上述操作后得到线段
上的每个点进行上述操作后得到线段 ,其中点
,其中点 的对应点分别为
的对应点分别为 .如图1,若点
.如图1,若点 表示的数是
表示的数是 ,则点
,则点 表示的数是 ;若点
表示的数是 ;若点 表示的数是2,则点
表示的数是2,则点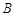 表示的数是 ;已知线段
表示的数是 ;已知线段 上的点
上的点 经过上述操作后得到的对应点
经过上述操作后得到的对应点 与点
与点 重合,则点
重合,则点 表示的数是 ;
表示的数是 ;
 中,对正方形
中,对正方形 及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数
及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一种实数 ,将得到的点先向右平移
,将得到的点先向右平移 个单位,再向上平移
个单位,再向上平移 个单位(
个单位( ),得到正方形
),得到正方形 及其内部的点,其中点
及其内部的点,其中点 的对应点分别为
的对应点分别为 。已知正方形
。已知正方形 内部的一个点
内部的一个点 经过上述操作后得到的对应点
经过上述操作后得到的对应点 与点
与点 重合,求点
重合,求点 的坐标。
的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com