
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,则BE与AF的数量关系是 .
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么上述结论还成立吗?请利用图②说明理由.

【答案】(1)BE=AF;(2)结论成立.理由见解析
【解析】
(1)证明△BDE≌△ADF(ASA),即可得出结论;
(2)证明△BDE≌△ADF(ASA),即可得出结论.
解:(1)BE=AF,理由如下:
连接AD.如图①所示:
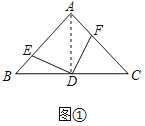
∵AB=AC,∠BAC=90°,点D为BC的中点,
∴AD⊥BC,AD=BD=CD,∠B=∠C=∠DAF=45°,
∵∠EDF=∠BDA=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中, ,
,
∴△BDE≌△ADF(ASA),
∴BE=DF;
故答案为:BE=AF.
(2)结论成立.理由如下:
连接AD,如图②所示:
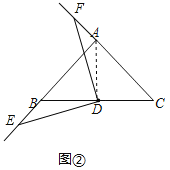
∵AB=AC,∠BAC=90°,BD=DC,
∴AD⊥BC,AD=BD=CD,∠B=∠C=∠DAC=45°,
∴∠DBE=∠DAF=135°,
∵∠EDF=∠BDA=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中,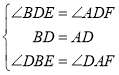 ,
,
∴△BDE≌△ADF(ASA),
∴BE=DF.


科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:(1)若![]() 的整数部分为
的整数部分为![]() ,小数部分为
,小数部分为![]() ,求
,求![]() 的值.
的值.
(2)已知:![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA切⊙O于A,AB⊥OP于B,若PO=8 cm,BO=2 cm,则PA的长为( ) 
A.16cm
B.48cm
C.6 ![]() cm
cm
D.4 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.
(1)请用a表示第三条边长;
(2)问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;
(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
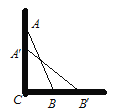
【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )

A.106cmB.110cmC.114cmD.116cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,AD=6m,CD=8m,BC=AB=13m,若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com