
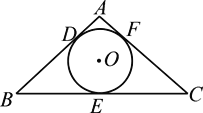
【题目】如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D,E,F.
(1)求证:BE=CE;
(2)若∠A=90°,AB=AC=2,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)利用切线长定理得出AD=AF,BD=BE,CE=CF,进而得出BD=CF,即可得出答案;
(2)首先连接OD、OE,进而利用切线的性质得出∠ODA=∠OFA=∠A=90°,进而得出四边形ODAF是正方形,再利用勾股定理求出⊙O的半径.
试题解析:(1)∵⊙O是△ABC的内切圆,切点为D、E、F,∴AD=AF,BD=BE,CE=CF.
∵AB=AC,∴AB-AD=AC-AF,即BD=CF.
∴BE=CE.
(2)如图,连接OD、OF,
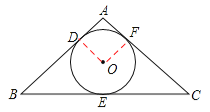
∵⊙O是△ABC的内切圆,切点为D、E、F,∴∠ODA=∠OFA=∠A=90°.
又OD=OF,∴四边形ODAF是正方形.
设OD=AD=AF=r,则BE=BD=CF=CE=![]() .
.
在△ABC中,∠A=90°,∴![]() .
.
又BC=BE+CE,∴![]() ,解得:r=
,解得:r=![]() .
.
∴⊙O的半径是![]() .
.


科目:初中数学 来源: 题型:
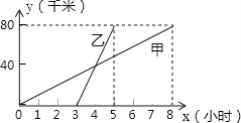
【题目】如图,甲、乙两人分别骑自行车和摩托车沿相同路线由A地到B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
(1)______先出发,提前______小时;
(2)______先到达B地,早到______小时;
(3)A地与B地相距______千米;
(4)甲乙两人在途中的速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

查看答案和解析>>
科目:初中数学 来源: 题型:
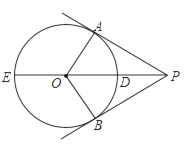
【题目】如图,PA、PB是⊙O的两条切线,切点分别为A、B,直线OP交⊙O于点D、E.
(1)求证:△PAO≌△PBO;
(2)已知PA=4,PD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读材料:实数的整数部分与小数部分
由于实数的小数部分一定要为正数,所以正、负实数的整数部分与小数部分确定方法存在区别:
⑴对于正实数,如实数9.23,在整数9—10之间,则整数部分为9,小数部分为9.23-9=0.23.
⑵对于负实数,如实数-9.23,在整数-10—-9之间,则整数部分为-10,小数部分为-9.23-(-10)=0.77.依照上面规定解决下面问题:
(1)已知![]() 的整数部分为a,小数部分为b,求a、b的值.
的整数部分为a,小数部分为b,求a、b的值.
(2)若x、y分别是8-![]() 的整数部分与小数部分,求
的整数部分与小数部分,求![]() 的值.
的值.
(3)设x=![]() , a是x的小数部分,b是 - x的小数部分.求
, a是x的小数部分,b是 - x的小数部分.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个实根x1和x2
(1) 求实数k的取值范围
(2) 若方程两实根x1、x2满足x12-x22=0,求k的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com