【题目】小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1 ， y1），P2（x2 ， y2），可通过构造直角三角形利用图1得到结论：P1P2= 他还利用图2证明了线段P1P2的中点P（x，y）P的坐标公式：x= ，y= ．

（1）请你帮小明写出中点坐标公式的证明过程；
（2）①已知点M（2，﹣1），N（﹣3，5），则线段MN长度为；
②直接写出以点A（2，2），B（﹣2，0），C（3，﹣1），D为顶点的平行四边形顶点D的坐标：；
（3）如图3，点P（2，n）在函数y= x（x≥0）的图象OL与x轴正半轴夹角的平分线上，请在OL、x轴上分别找出点E、F，使△PEF的周长最小，简要叙述作图方法，并求出周长的最小值．

参考答案：

【答案】
（1）

证明：∵P1（x1，y1），P2（x2，y2），

∴Q1Q2=OQ2﹣OQ1=x2﹣x1，

∴Q1Q= ，

∴OQ=OQ1+Q1Q=x1+ = ，

∵PQ为梯形P1Q1Q2P2的中位线，

∴PQ= = ，

即线段P1P2的中点P（x，y）P的坐标公式为x= ，y=


（2） ；（﹣3，3）或（7，1）或（﹣1，﹣3）
（3）

解：如图，设P关于直线OL的对称点为M，关于x轴的对称点为N，连接PM交直线OL于点R，连接PN交x轴于点S，连接MN交直线OL于点E，交x轴于点F，

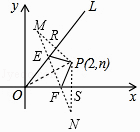
又对称性可知EP=EM，FP=FN，

∴PE+PF+EF=ME+EF+NF=MN，

∴此时△PEF的周长即为MN的长，为最小，

设R（x， x），由题意可知OR=OS=2，PR=PS=n，

∴ =2，解得x=﹣ （舍去）或x= ，

∴R（ ， ），

∴ =n，解得n=1，

∴P（2，1），

∴N（2，﹣1），

设M（x，y），则 = ， = ，解得x= ，y= ，

∴M（ ， ），

∴MN= = ，

即△PEF的周长的最小值为


【解析】（2）①∵M（2，﹣1），N（﹣3，5），
∴MN= = ，
所以答案是： ；
②∵A（2，2），B（﹣2，0），C（3，﹣1），
∴当AB为平行四边形的对角线时，其对称中心坐标为（0，1），
设D（x，y），则x+3=0，y+（﹣1）=2，解得x=﹣3，y=3，
∴此时D点坐标为（﹣3，3），
当AC为对角线时，同理可求得D点坐标为（7，1），
当BC为对角线时，同理可求得D点坐标为（﹣1，﹣3），
综上可知D点坐标为（﹣3，3）或（7，1）或（﹣1，﹣3），
所以答案是：（﹣3，3）或（7，1）或（﹣1，﹣3）；
【考点精析】根据题目的已知条件，利用勾股定理的概念和轴对称-最短路线问题的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．

关闭