
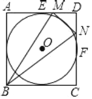
【题目】如图,⊙O内切于正方形ABCD,边AD、CD分别与⊙O切于点E、F,点M、N分别在线段DE、DF上,且MN与⊙O相切,若△MBN的面积为8,则⊙O的半径为( )
A.![]() B.2
B.2![]() C.
C.![]() D.2
D.2![]()
【答案】B
【解析】
设⊙O与MN相切于点K,设正方形的边长为2a.因为AD、CD、MN是切线,可得AE=DE=DF=CF=a,MK=ME,NK=NF,设MK=ME=x,NK=NF=y,在Rt△DMN中,以为MN=x+y,DN=a-y,DM=a-x,看到(x+y)2=(a-y)2+(a-x)2,推出ax+ay+xy=a2,根据S△BMN=S正方形ABCD-S△ABM-S△DMN-S△BCN=8,构建方程求出a即可解决问题;
解:设⊙O与MN相切于点K,设正方形的边长为2a.
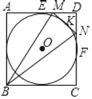
∵AD、CD、MN是切线,
∴AE=DE=DF=CF=a,MK=ME,NK=NF,设MK=ME=x,NK=NF=y,
在Rt△DMN中,∵MN=x+y,DN=a﹣y,DM=a﹣x,
∴(x+y)2=(a﹣y)2+(a﹣x)2,
∴ax+ay+xy=a2,
∵S△BMN=S正方形ABCD﹣S△ABM﹣S△DMN﹣S△BCN=8,
∴4a2﹣![]() ×2a×(a+x)﹣
×2a×(a+x)﹣![]() (a﹣x)(a﹣y)﹣
(a﹣x)(a﹣y)﹣![]() ×2a×(a+y)=8,
×2a×(a+y)=8,
∴![]() a2﹣
a2﹣![]() (ax+ay+xy)=8,
(ax+ay+xy)=8,
∴a2=8,
∴a=2![]() ,
,
∴AB=2a=4![]() ,
,
∴⊙O的半径为2![]() ,
,
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于点A(﹣2,0)与点C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
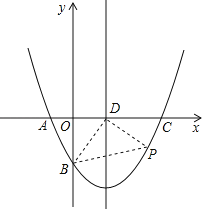
(1)直接写出B点的坐标;
(2)求该二次函数的解析式;
(3)若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,AB.请问是否存在点P,使得△BDP的面积恰好等于△ADB的面积?若存在请求出此时点P的坐标,若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球是等可能的,你同意他的说法吗?为什么?
(2)搅匀后从中一把摸出两个球,请通过列表和树状图求出两个球都是白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,∠E=30°,AC=5.
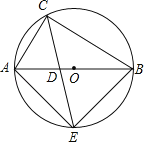
(1)求CE的长;
(2)求S△ADC:S△ACE的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
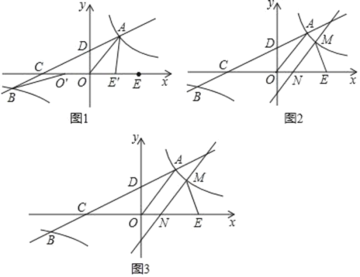
【题目】如图1,在平面直角坐标系xOy中,双曲线![]() 与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
(1)将线段OE沿x轴平移得线段O′E′(如图1),在移动过程中,是否存在某个位置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此时点O′的坐标;若不存在,请说明理由;
(2)将直线OA沿射线OE平移,平移过程中交![]() 的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,我们规定:一个锐角的对边与斜边的比值称为这个锐角的正弦值.
例如:Rt△ABC中,∠C=90°,∠A的对边BC与斜边AB的比值,即![]() 就是∠A的正弦值.利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:
就是∠A的正弦值.利用量角器可以制作“锐角正弦值速查卡”.制作方法如下:
如图,设OA=1,以O为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,再以OA为直径作⊙M.利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值.例如:60°的正弦值约在0.85~0.88之间取值,45°的正弦值约在0.70~0.72之间取值.下列角度中正弦值最接近0.94的是( )
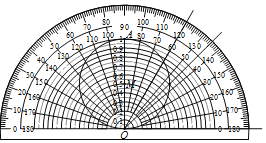
A.30°B.50°C.40°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随点
的位置随点![]() 的位置变化而变化.
的位置变化而变化.
(1)如图1,当点![]() 在菱形
在菱形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是 ,
的数量关系是 ,![]() 与
与![]() 的位置关系是 ;
的位置关系是 ;
(2)当点![]() 在菱形
在菱形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,
请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3) 如图4,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
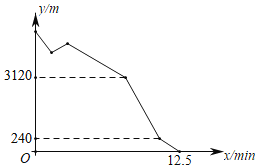
【题目】10月期间,我市庆祝新中国成立70周年“祖国万岁”的主题灯光秀展示了两江四岸流光溢彩的壮美之景.周末,小明和小华相约一起乘轻轨去看灯光秀.已知小明家、轻轨站和小华家顺次分布在同一条笔直的公路上.小明、小华打算以各自的速度步行到轻轨站,小明出发3分钟后,小华从家里出发,走了两分钟,小华想起没带相机,立即掉头以原速的![]() 返回家中取相机,并在家中取停留5分钟,发现时间来不及便立即打车前住轻轨站,最终比小明早到2分钟.如图是两人之间的距离与小华出发时间之间的关系,则小明家离轻轨站的距离比小华家离轻轨站的距离少_____米.
返回家中取相机,并在家中取停留5分钟,发现时间来不及便立即打车前住轻轨站,最终比小明早到2分钟.如图是两人之间的距离与小华出发时间之间的关系,则小明家离轻轨站的距离比小华家离轻轨站的距离少_____米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com