
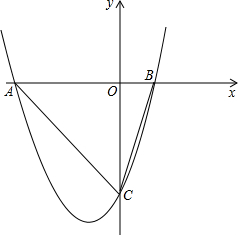
 已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.
已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.分析 (1)在y=x2+2x-3中令y=3可求得A、B坐标,再利用待定系数法可求得直线AC的解析式;
(2)可求得点B关于直线x=-2的对称点B′的坐标,连接B′C,交直线x=-2于点D,则D满足条件,利用待定系数法可求得直线B′C的解析式,令x=-2可求得a的值;
(3)可设出P点坐标,可表示出AP、AO、AB、AC的长,当△AOP和△ABC相似时,分两种情况△APO∽△ACB和△APO∽△ABC,再利用相似三角形的性质可分别求得P点坐标.
解答 解:(1)在y=x2+2x-3中,令y=0可得x2+2x-3=0,解得x=-3或x=1,
∴A(-3,0),B(1,0),且C(0,-3),
设直线AC解析式为y=kx+b,把A、C坐标代入可得$\left\{\begin{array}{l}{0=-3k+b}\\{-3=b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$,
∴直线AC的解析式为y=-x-3,
故答案为:1;0;-x-3;
(2)由题意可知点D在直线x=-2上,
∵B(1,0),
∴点B关于直线x=-2的对称点B′的坐标为(-5,0),
连接B′C,交直线x=-2于点D,如图1,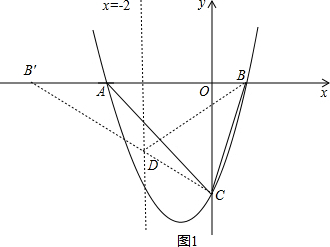
则BD=B′D,
∴BD+CD=B′D+CD=B′C,
∴此时BD+CD最小,
设直线B′C的解析式为y=mx+n,把B′、C的坐标代入可得$\left\{\begin{array}{l}{0=-5m+n}\\{-3=n}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-\frac{3}{5}}\\{n=-3}\end{array}\right.$,
∴直线B′C的解析式为y=-$\frac{3}{5}$x-3,
把D点坐标代入可得a=-$\frac{3}{5}$×(-2)-3=-$\frac{9}{5}$,
即a的值为-$\frac{9}{5}$;
(3)∵P点在直线AC上,
∴可设P点坐标为(x,-x-3),
由条件可知P点只能在线段AC上,
∴-3<x<0,
∴x+3>0,
∴AO=3,AB=4,AC=3$\sqrt{2}$,AP=$\sqrt{(x+3)^{2}+(-x-3)^{2}}$=$\sqrt{2}$(x+3),
当△AOP和△ABC相似时,有两种情况:即△APO∽△ACB和△APO∽△ABC,
当△APO∽△ACB时,则有$\frac{AP}{AC}$=$\frac{AO}{AB}$,即$\frac{\sqrt{2}(x+3)}{3\sqrt{2}}$=$\frac{3}{4}$,解得x=-$\frac{3}{4}$,此时P点坐标为(-$\frac{3}{4}$,-$\frac{9}{4}$);
当△APO∽△ABC时,则有$\frac{AP}{AB}$=$\frac{AO}{AC}$,即$\frac{\sqrt{2}(x+3)}{4}$=$\frac{3}{3\sqrt{2}}$,解得x=-1,此时P点坐标为(-1,-2);
综上可知存在满足条件的点P,其坐标为(-$\frac{3}{4}$,-$\frac{9}{4}$)或(-1,-2).
点评 本题主要考查二次函数的综合应用,涉及待定系数法、轴对称的性质、相似三角形的判定和性质等知识点.在(1)中注意二次函数与一元二次方程的关系的应用,在(2)中确定出D点的位置是解题的关键,在(3)中分两种情况进行求解是解题的关键.本题考查知识比较基础,难度不大.


科目:初中数学 来源: 题型:解答题
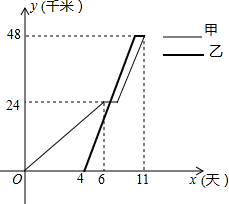 甲、乙两工程队维修同样长度的两段公路,甲队每天完成a千米,中间因故停工一段时间,之后又以每天2a千米的速度继续工作;乙队在甲队工作4天后开始工作,比甲队早一天完成任务.设甲、乙两工程队各自完成任务的工作量为y(千米),甲队的工作时间为x(天).当0≤x≤11时,y与x之间的函数图象如图所示.
甲、乙两工程队维修同样长度的两段公路,甲队每天完成a千米,中间因故停工一段时间,之后又以每天2a千米的速度继续工作;乙队在甲队工作4天后开始工作,比甲队早一天完成任务.设甲、乙两工程队各自完成任务的工作量为y(千米),甲队的工作时间为x(天).当0≤x≤11时,y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 农作物 | 每公顷所需工人数/人 | 每公顷预计产值/万元 |
| 水稻 | 4 | 4.5 |
| 蔬菜 | 8 | 9 |
| 棉花 | 5 | 7.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
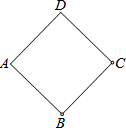 如图,正方形ABCD,边长AB=2.
如图,正方形ABCD,边长AB=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
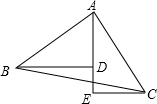 如图,A、D、E三点在同一条直线上,且△BAD≌△ACE.
如图,A、D、E三点在同一条直线上,且△BAD≌△ACE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
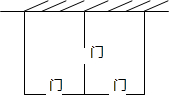 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为75m2.
某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门.已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为75m2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
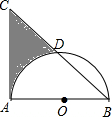 如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )| A. | 24-4π | B. | 32-4π | C. | 32-8π | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com