
【题目】在长方形ABCD中,长方形ABCD的周长为36厘米,BC比AB大2厘米.点E在线段AB上,且AE=3BE,动点P从A点出发,在线段AD上以每秒1厘米的速度向终点D运动;动点Q从C点出发,沿着射线CB以每秒5厘米的速度运动,三角形APE的面积为S1,三角形EBQ的面积为S2,两点同时出发,当一个点停止运动时,另一个点也停止运动,设它们运动的时间为t秒.
(1)求AB、BC的长;
(2)请用含t的式子分别表示S1和S2;
(3)它们出发几秒时,S1=S2?
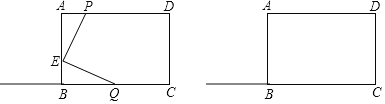
【答案】(1)AB=8厘米,BC=10厘米;(2)S1=3t(厘米2),S2=(10﹣5t)(厘米2);(3)P、Q出发![]() 秒或5秒时,S1=S2
秒或5秒时,S1=S2
【解析】
(1)由矩形的性质得出AB=CD,AD=BC,由题意得出AD=BC=AB+2,由矩形ABCD的周长得出2(AB+BC)=36,求解即可;
(2)由题意得AP=t,CQ=5t,求出BE=2,AE=6,由三角形面积公式得出即可求解;
(3)由题意得出方程3t=10﹣5t或3t=5t﹣10,解方程即可.
(1)∵四边形ABCD是矩形,
∴AB=CD,AD=BC,
由题意得:AD=BC=AB+2,
∵矩形ABCD的周长为36,
∴2(AB+BC)=36,
即2(AB+AB+2)=36,
解得:AB=8,则BC=10,
答:AB=8厘米,BC=10厘米;
(2)由题意得:AP=t,CQ=5t,
∴BQ=10﹣5t,
∵AE=3BE,AB=8,
∴BE=2,AE=6,
∴S1=![]() AE×AP=
AE×AP=![]() ×6×t=3t(厘米2),
×6×t=3t(厘米2),
S2=![]() BE×BQ=
BE×BQ=![]() ×2×(10﹣5t)= (10﹣5t)(厘米2);
×2×(10﹣5t)= (10﹣5t)(厘米2);
(3)∵S1=S2,
∴3t=10﹣5t或3t=5t﹣10,
解得:t=![]() 或t=5,
或t=5,
即P、Q出发![]() 秒或5秒时,S1=S2.
秒或5秒时,S1=S2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
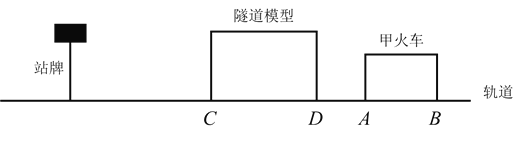
【题目】小明有一套火车玩具,有两列火车、一副轨道、一个隧道模型及一个站牌.特别之处:隧道模型也可以像火车一样移动,当火车头进入隧道一瞬间会响起音乐,当火车完全穿过隧道的一瞬间音乐会结束.已知甲火车长![]() 厘米,甲乙两列火车的速度均为
厘米,甲乙两列火车的速度均为![]() 厘米/秒,轨道长
厘米/秒,轨道长![]() 米.
米.
(1)将轨道围成一个圆圈,将甲、乙两列火车紧挨站牌放置,车头方向相反,同时启动,到两车相撞用时![]() 秒,求乙火车的长度?
秒,求乙火车的长度?
(2)在(1)的条件下,乙火车穿过静止的隧道音乐响起了![]() 秒,求隧道的长度;
秒,求隧道的长度;
(3)在(1)(2)的条件下,轨道铺成一条直线,把隧道模型、甲火车依次放在站牌的右侧,站牌静止不动,甲火车头与隧道相距![]() (即
(即![]() ).当甲火车向左运动,隧道模型以不变的速度运动,音乐却响了
).当甲火车向左运动,隧道模型以不变的速度运动,音乐却响了![]() 秒;当音乐结束的一瞬间,甲火车头
秒;当音乐结束的一瞬间,甲火车头![]() 与站牌相距乙火车车身的长度,请同学们思考一下,以站牌所在地为原点建立数轴,你能确定甲火车、隧道在运动前的位置吗?如果可以,请画出数轴并标出
与站牌相距乙火车车身的长度,请同学们思考一下,以站牌所在地为原点建立数轴,你能确定甲火车、隧道在运动前的位置吗?如果可以,请画出数轴并标出![]() 运动前的位置.
运动前的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市十一优惠顾客,若一次性购物不超过300元不优惠,超过300元时按全额9折优惠.一位顾客第一次购物付款120元,第二次购物付款288元,若这两次购物合并成一次性付款可节省_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,AD=DC,点F在AD上,AB=FC,BF的延长线交AC于点E.
(1)求证:△ABD≌△CFD.
(2)求证:CF⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华与爸爸用一个如图所示的五等分、可以自由转动的转盘来玩游戏;将转盘随机转一次,指针指向的数字如果是奇数.爸爸获胜,如果是偶数,则小华获胜(指针指到线上则重转)
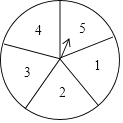
(1)转完转盘后指针指向数字2的概率是多少?
(2)这个游戏公平吗?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
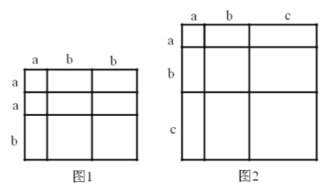
【题目】阅读下列文字,对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如:由图1可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决问题:已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com