Question

2．已知点A、B、C是直径为6cm的⊙O上的点，且AB=3cm，AC=3$\sqrt{2}$cm，则∠BAC的度数为（　　）

• A． 15°
• B． 75°或15°
• C． 105°或15°
• D． 75°或105°

Answer 1

分析 从弦AB、AC在直径AD的同旁和两旁两种情况进行计算，根据特殊角的三角函数值分别求出∠BAD和∠CAD的度数，计算得到答案．

解答 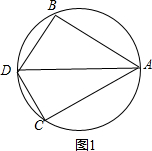解：如图1，∵AD为直径，
∴∠ABD=∠ACD=90°，
在Rt△ABD中，AD=6，AB=3，
则∠BDA=30°，∠BAD=60°，
在Rt△ABD中，AD=6，AB=3$\sqrt{2}$，
∠CAD=45°，
则∠BAC=105°；
如图2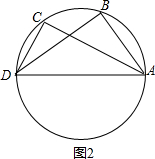，，∵AD为直径，
∴∠ABD=∠ABC=90°，
在Rt△ABD中，AD=6，AB=3，
则∠BDA=30°，∠BAD=60°，
在Rt△ABC中，AD=6，AB=3$\sqrt{2}$，
∠CAD=45°，
则∠BAC=15°，
故选：C．

点评 本题考查的是圆周角定理和锐角三角函数的知识，掌握直径所对的圆周角是直径和熟记特殊角的三角函数值是解题的关键，注意分情况讨论思想的运用．