
 为迎接“六一儿童节”,小天使培训班准备购买“悠悠兔卷笔刀”作为节日礼物送给小朋友.经调查发现:在“丽水沃尔玛超市”悠悠兔卷笔刀的单价为4元/个;在淘宝网店购买,同牌子卷笔刀的价格是超市的8.5折,但需快递费15元.
为迎接“六一儿童节”,小天使培训班准备购买“悠悠兔卷笔刀”作为节日礼物送给小朋友.经调查发现:在“丽水沃尔玛超市”悠悠兔卷笔刀的单价为4元/个;在淘宝网店购买,同牌子卷笔刀的价格是超市的8.5折,但需快递费15元.分析 (1)根据购买费用=单价×数量+快递费,建立关系就可以表示出y1、y2的解析式;
(2)分三种情况进行讨论:当y1>y2时,当y1=y1时,当y1<y2时,分别求出购买划算的方案.
解答 解:(1)由题意,得y1=4x,y=3.4x+15;
(2)∵当y1>y2时,即4x>3.4x+15,则x>25;
当y1=y2时,即4x=3.4x+15,则x=25;
当y1<y2时,即4x<3.4x+15,则x<25;
∴该培训班购买卷笔刀的数量大于25个时应选择网购合算,
当购买卷笔刀的数量小于25个时应选择超市购买合算,
当购买卷笔刀的数量等于25个时选择两种购买方式一样合算.
点评 本题考查了一次函数的解析式的运用,分类讨论的数学思想的运用,方案设计的运用,解答时求出函数的解析式是关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
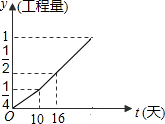 甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程.设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少12天.
甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程.设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少12天.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 15° | B. | 75°或15° | C. | 105°或15° | D. | 75°或105° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
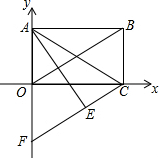 如图,平面直角坐标系中,A、C两点的坐标分别是A(0,4),C(8,0),以OA、OC为邻边作矩形OABC,然后以AC为折痕折叠矩形,使B点落在第四象限的E处,AE交x轴于D点,连接CE并延长交y轴于F点.
如图,平面直角坐标系中,A、C两点的坐标分别是A(0,4),C(8,0),以OA、OC为邻边作矩形OABC,然后以AC为折痕折叠矩形,使B点落在第四象限的E处,AE交x轴于D点,连接CE并延长交y轴于F点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com