
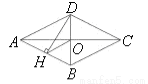
如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:
∠DHO=∠DCO.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:青岛版八年级下6.2平行四边形的判定 题型:选择题
不能判定一个四边形是平行四边形的条件是( )
A.两组对边分别平行
B.一组对边平行另一组对边相等
C.一组对边平行且相等
D.两组对边分别相等
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:选择题
如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD,BC于E,F点,连接CE,则△CDE的周长为( )

A.5cm B.8cm C.9cm D.10cm
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:填空题
如图,矩形ABCD的面积为5,它的两条对角线交于点O1,以AB,AO1为两邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2,同样以AB,AO2为两邻边作平行四边形ABC2O2,…,依此类推,则平行四边形ABCnOn的面积为_______.

查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.3特殊的平行四边形 题型:选择题
如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )

A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:选择题
如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )
A. B.
B. C.3 D.4
C.3 D.4
查看答案和解析>>
科目:初中数学 来源:青岛版八年级下6.4三角形的中位线 题型:选择题
如图,已知四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大
B.线段EF的长逐渐减少
C.线段EF的长不变
D.线段EF的长与点P的位置有关
查看答案和解析>>
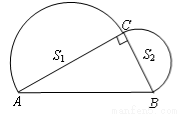
科目:初中数学 来源:青岛版八年级下7.2勾股定理 题型:填空题
如图,已知在Rt△ABC中,∠ACB=Rt∠,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com