
【题目】五一期间,乐乐与小佳两个人打算骑共享单车骑行出游,两人打开手机![]() 进行选择,已知附近共有3种品牌的4辆车,其中
进行选择,已知附近共有3种品牌的4辆车,其中![]() 品牌有2辆,
品牌有2辆,![]() 品牌和
品牌和![]() 品牌各有1辆,手机上无法识别品牌,且有人选中车后其他人无法再选.
品牌各有1辆,手机上无法识别品牌,且有人选中车后其他人无法再选.
(1)若乐乐首先选择,求乐乐选中![]() 品牌单车的概率;
品牌单车的概率;
(2)请用画树状图或列表的方法求乐乐和小佳选中同一品牌单车的概率.
科目:初中数学 来源: 题型:
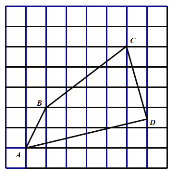
【题目】如图,在每个小正方形的边长为的网格中,点![]() 均在格点上,
均在格点上,![]() 为小正方形边中点.
为小正方形边中点.
(1)![]() 的长等于 ______;
的长等于 ______;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个点![]() ,使其满足
,使其满足![]() 说明点
说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的图形W1和图形W2.给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系
(1)如图1,点C(1,0),D(-1,0),E(0,![]() ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
①线段OP的最小值为_______,最大值为_______;线段CP的取值范直范围是_____;
②在点O,点C中,点____________与线段DE满足限距关系;
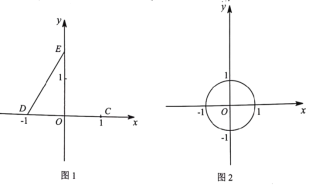
(2)如图2,⊙O的半径为1,直线![]() (b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;
(3)⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H和K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
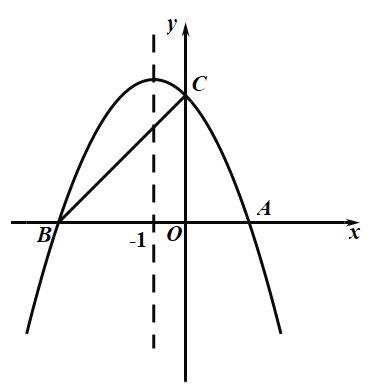
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,它的对称轴是直线
,它的对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 为等腰三角形,请求出符合条件的所有点
为等腰三角形,请求出符合条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
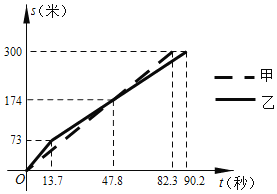
【题目】甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,根据图象有以下四个判断:
①乙队率先到达终点;
②甲队比乙队多走了126米;
③在47.8秒时,两队所走路程相等;
④从出发到13.7秒的时间段内,甲队的速度比乙队的慢.
所有正确判断的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
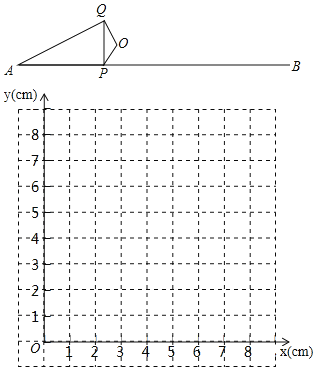
【题目】如图,P是线段AB上的一点,AB=6cm,O是AB外一定点.连接OP,将OP绕点O顺时针旋转120°得OQ,连接PQ,AQ.小明根据学习函数的经验,对线段AP,PQ,AQ的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,PQ,AQ的长度(单位:cm)的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP,PQ,AQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;/span>
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当AQ=PQ时,线段AP的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
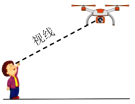
【题目】为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为![]() ,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:
,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y1=x(x<m)的图象与函数y2=x2(x≥m)的图象组成图形G.对于任意实数n,过点P(0,n)且与x轴平行的直线总与图形G有公共点,写出一个满足条件的实数m的值为_____(写出一个即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com